题目内容
14.先化简,再求x=6时的值:($\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$)$÷\frac{x+2}{{x}^{3}-4x}$.分析 根据分式的减法和除法可以化简题目中的式子,然后将x=6代入化简后的式子即可解答本题.
解答 解:($\frac{x+2}{{x}^{2}-2x}$-$\frac{x-1}{{x}^{2}-4x+4}$)$÷\frac{x+2}{{x}^{3}-4x}$
=$\frac{(x+2)(x-2)-x(x-1)}{x(x-2)^{2}}•\frac{x(x+2)(x-2)}{x+2}$
=$\frac{-3}{x(x-2)^{2}}•\frac{x(x+2)(x-2)}{x+2}$
=$\frac{-3}{x-2}$,
当x=6时,原式=$\frac{-3}{6-2}=-\frac{3}{4}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式的化简求值的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.下列各组线段中,能构成直角三角形的一组是( )
| A. | 5,9,12 | B. | 7,12,13 | C. | 0.3,0.4,0.5 | D. | 3,4,6 |
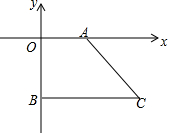 如图,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于点B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16,求C点坐标.
如图,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于点B(0,b),且(a-3)2+|b+4|=0,S四边形AOBC=16,求C点坐标.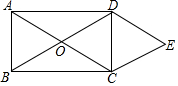 如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2.求四边形OCED的面积.
如图,矩形ABCD的对角线AC与BD相交于点O,CE∥BD,DE∥AC,AD=2$\sqrt{3}$,DE=2.求四边形OCED的面积.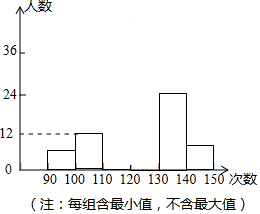 4月22日,垦利区九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频数和是18,乙同学计算出第一组的人数是抽取总人数的4%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题:
4月22日,垦利区九年级学生进行了中考体育测试,某校抽取了部分学生的一分钟跳绳测试成绩,将测试成绩整理后作出如下统计图.甲同学计算出前两组的频数和是18,乙同学计算出第一组的人数是抽取总人数的4%,丙同学计算出从左至右第二、三、四组的频数比为4:17:15.结合统计图回答下列问题: