题目内容
20.列方程解应用题:10月9日,金秋的北京.我校初二全体同学到距学校30公里的房山农业职业学院,参加为期一周的学农劳动.同学们乘坐大巴车前往,李老师因学校有事晚出发了5分钟,开私家车前往.结果和同学们同时到达了农职院.已知李老师开的私家车的速度是大巴车速度的1.2倍.求大巴车和李老师开的私家车的速度分别是多少?
分析 设设大巴车的速度是x千米/小时,根据题意列出方程解答即可.
解答 解:设大巴车的速度是x千米/小时,
$\frac{30}{x}-\frac{30}{1.2x}=\frac{5}{60}$
解得:x=60
经检验x=60是原方程的解且符合题意.
1.2x=72;
答:大巴车和李老师开的私家车的速度分别是60千米/小时和72千米/小时.
点评 本题考查分式方程的应用,关键以时间做为等量关系列方程求解.

练习册系列答案
相关题目
12.下列函数中,是正比例函数的是( )
| A. | y=$\frac{x}{2}$ | B. | y=$\frac{-2}{x}$ | C. | y=2x2+1 | D. | y=$\frac{1}{2}$x-1 |
13.关于函数y=2x2-3,y=-$\frac{1}{2}{x^2}$的图象及性质,下列说法不正确的是( )
| A. | 它们的对称轴都是y轴 | |
| B. | 对于函数$y=-\frac{1}{2}{x^2}$,当x>0时,y随x的增大而减小 | |
| C. | 抛物线y=2x2-3不能由抛物线y=-$\frac{1}{2}{x^2}$平移得到 | |
| D. | 抛物线y=2x2-3的开口比y=-$\frac{1}{2}{x^2}$的开口宽 |
5.已知A、B、C三点在⊙O上,且AB是⊙O内接正三角形的边长,AC是⊙O内接正方形的边长,则∠BAC的度数为( )
| A. | 15°或105° | B. | 75°或15° | C. | 75° | D. | 105° |
11. 如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
 如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
如图,在△ABC中,AB=AC,∠A=50°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
9.如果$\sqrt{(2a-1)^{2}}$=2a-1,那么a的取值范围( )
| A. | a>$\frac{1}{2}$ | B. | a<$\frac{1}{2}$ | C. | a≥$\frac{1}{2}$ | D. | a≤$\frac{1}{2}$ |
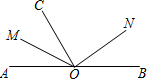 如图,O是直线AB上一点,OM平分∠AOC、ON平分∠BOC.
如图,O是直线AB上一点,OM平分∠AOC、ON平分∠BOC.