题目内容
16．
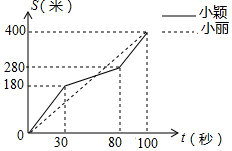小丽和小颖进行400米耐力测试，他们同时起跑，同时到达终点，所跑的路程y（米）与所用时间t（秒）之间的关系如图所示，则他们第一次相遇的时间是起跑后第60秒．
分析 分别求出OA、BC的解析式，然后联立方程，解方程就可以求出第一次相遇时间．
解答 
解：设直线OA的解析式为y=kx，
代入A（100，400）得400=100k，
解得k=4，
故直线OA的解析式为y=4x，
设BC的解析式为y1=k1x+b，由题意，得
$\left\{\begin{array}{l}{180=30{k}_{1}+b}\\{280=80{k}_{1}+b}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{{k}_{1}=2}\\{b=120}\end{array}\right.$，
∴BC的解析式为y1=2x+120，
当y=y1时，4x=2x+120，
解得：x=60．
故她们第一次相遇的时间是起跑后的第60秒．
故答案为：60．
点评 本题考查了一次函数的运用，一次函数的图象的意义的运用，待定系数法求一次函数的解析式的运用，利用函数图象交点的实际意义是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
，则x的范围是_____________。
电力公司为鼓励市民节约用电，采取按月用电量分段收费办法．若某户居民每月应交电费y（元）与用电量x（度）的函数图象是一条折线（如图所示），根据图象解下列问题：
12．
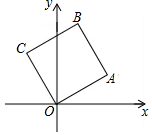如图，点A在第一象限内，其坐标为（2，1），以OA为边在x轴上方作正方形OABC，则正方形OABC的顶点C的坐标是（ ）
如图，点A在第一象限内，其坐标为（2，1），以OA为边在x轴上方作正方形OABC，则正方形OABC的顶点C的坐标是（ ）| A． | （-2，1） | B． | （1，3） | C． | （1，2） | D． | （-1.2） |
1．
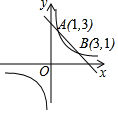函数y1=$\frac{k}{x}$与y2=ax+b的图象在同一直角坐标系中如图所示，当y1＜y2时，x的取值范围是（ ）
函数y1=$\frac{k}{x}$与y2=ax+b的图象在同一直角坐标系中如图所示，当y1＜y2时，x的取值范围是（ ）| A． | 1＜x＜3 | B． | x＜1 | C． | x＜0或1＜x＜3 | D． | x＜1或x＞3 |
如图，在平面直角坐标系中，△ABC的三个顶点坐标分别是A（-3，2），B（-1，4），C（0，2）