题目内容
8.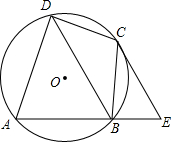 如图,四边形ABCD为⊙O的内接四边形,CE∥DB交AB的延长线于E,求证:BC•CD=DA•BE.
如图,四边形ABCD为⊙O的内接四边形,CE∥DB交AB的延长线于E,求证:BC•CD=DA•BE.
分析 连接AC,由四边形ABCD为⊙O的内接四边形,得到∠CBE=∠ADC,根据平行线的性质得到∠DBC=∠BCE,根据圆周角定理得到∠DAC=∠DBC,等量代换得到∠CBE=∠DAC,推出△ADC∽△CBE,根据相似三角形的性质即可得到结论.
解答 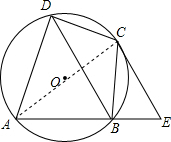 证明:连接AC,
证明:连接AC,
∵四边形ABCD为⊙O的内接四边形,
∴∠CBE=∠ADC,
∵CE∥BD,
∴∠DBC=∠BCE,
∵∠DAC=∠DBC,
∴∠CBE=∠DAC,
∴△ADC∽△CBE,
∴$\frac{AD}{BC}=\frac{CD}{BE}$,
∴BC•CD=DA•BE.
点评 本题考查了相似三角形的判定和性质,圆内接四边形的性质,圆周角定理,连接AC构造相似三角形是解题的关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
18.下列图形中,对角互补的是( )
| A. | 平行四边形 | B. | 直角梯形 | C. | 等腰梯形 | D. | 梯形 |
13.钟面角是指时钟的时针与分针所成的角.从上午8点整到上午11点整,钟面角为90°的情况出现了( )
| A. | 6次 | B. | 5次 | C. | 4次 | D. | 3次 |
 如图,已知圆锥的母线长为9m,底面半径是4m,则圆锥的侧面积是36πm2.
如图,已知圆锥的母线长为9m,底面半径是4m,则圆锥的侧面积是36πm2.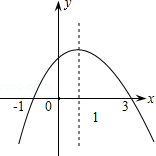 如图是二次函数y=ax2+bx+c的图象,下列结论:
如图是二次函数y=ax2+bx+c的图象,下列结论: