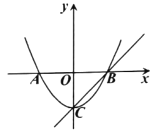
ƒøƒĞ»ı
°æƒø°ø–¬∂®“£∫∂‘”Ğπÿ”Ğ![]() µƒ∫Ø ˝
µƒ∫Ø ˝![]() Œ“√«≥∆∫Ø ˝
Œ“√«≥∆∫Ø ˝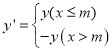 Œ™∫Ø ˝
Œ™∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝(∆‰÷–
∑÷∫Ø ˝(∆‰÷–![]() Œ™≥£ ˝)£Æ
Œ™≥£ ˝)£Æ
¿˝»Á£∫∂‘”Ğπÿ”Ğ![]() µƒ“ª¥Œ∫Ø ˝
µƒ“ª¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝Œ™
∑÷∫Ø ˝Œ™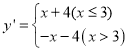
£®1£©»Ùµ„![]() ‘Ğπÿ”Ğ
‘Ğπÿ”Ğ![]() µƒ“ª¥Œ∫Ø ˝
µƒ“ª¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝…œ£¨«Û
∑÷∫Ø ˝…œ£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
£®2£©–¥≥ˆ∑¥±»¿˝∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝µƒÕºœÛ…œ
∑÷∫Ø ˝µƒÕºœÛ…œ![]() ÀÊ
ÀÊ![]() µƒ‘ˆ¥Û∂¯º–°µƒ
µƒ‘ˆ¥Û∂¯º–°µƒ![]() µƒ»°÷µ∑∂Œß £ª
µƒ»°÷µ∑∂Œß £ª
£®3£©»Ù![]() «∂˛¥Œ∫Ø ˝
«∂˛¥Œ∫Ø ˝![]() πÿ”Ğ
πÿ”Ğ![]() µƒ
µƒ![]() ∑÷∫Ø ˝£Æ
∑÷∫Ø ˝£Æ
![]() µ±
µ±![]() ±£¨«Û
±£¨«Û![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
![]() µ±
µ±![]() ±£¨
±£¨![]() ‘Ú
‘Ú![]() µƒ»°÷µ∑∂ŒßŒ™ £ª
µƒ»°÷µ∑∂ŒßŒ™ £ª
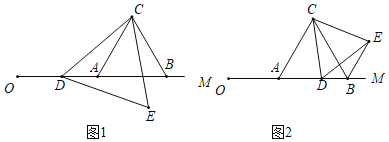
£®4£©»Ùµ„![]() ¡¨Ω·
¡¨Ω·![]() µ±πÿ”Ğ
µ±πÿ”Ğ![]() µƒ∂˛¥Œ∫Ø ˝
µƒ∂˛¥Œ∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝£¨”Îœş∂Œ
∑÷∫Ø ˝£¨”Îœş∂Œ![]() ”–¡Ω∏ˆΩªµ„£¨÷±Ω”–¥≥ˆ
”–¡Ω∏ˆΩªµ„£¨÷±Ω”–¥≥ˆ![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
°æ¥∞∏°ø£®1£©![]() £®2£©
£®2£©![]() ªÚ
ªÚ![]() £®3£©¢Ÿ
£®3£©¢Ÿ![]() ªÚ
ªÚ![]() ¢Ğ
¢Ğ![]() £®4£©m£º1ªÚ
£®4£©m£º1ªÚ![]() °İm£º
°İm£º![]() ªÚm°ı4
ªÚm°ı4
°æΩ‚Œˆ°ø
£®1£©∏˘æı“‚–¥≥ˆ“ª¥Œ∫Ø ˝y£Ωx£´1µƒ2∑÷∫Ø ˝Œ™y'£¨∞—x=4¥˙»Îº¥ø…«ÛΩ‚£ª
£®2£©∏˘æı“‚–¥≥ˆ∑¥±»¿˝∫Ø ˝![]() µƒ
µƒ![]() ∑÷∫Ø ˝y'£¨∏˘æı∑¥±»¿˝∫Ø ˝µƒÕºœÒº¥ø…≈–∂œ£ª
∑÷∫Ø ˝y'£¨∏˘æı∑¥±»¿˝∫Ø ˝µƒÕºœÒº¥ø…≈–∂œ£ª
£®3£©¢Ÿ∏˘æı“‚–¥≥ˆ∂˛¥Œ∫Ø ˝![]() πÿ”Ğ
πÿ”Ğ![]() µƒ
µƒ![]() ∑÷∫Ø ˝y'£¨∏˘æı
∑÷∫Ø ˝y'£¨∏˘æı![]() ∑÷∂Œº¥ø…«ÛΩ‚£ª
∑÷∂Œº¥ø…«ÛΩ‚£ª
¢Ğ ◊œ»«Û≥ˆµ±![]() ±£¨
±£¨![]() µƒ»°÷µ∑∂ŒßŒ™
µƒ»°÷µ∑∂ŒßŒ™![]() £¨µ±
£¨µ±![]() ±£¨
±£¨![]() ø…÷™£¨«Û≥ˆ
ø…÷™£¨«Û≥ˆ![]() ±
±![]() µƒ÷µ‘Ğ-3∫Õ-4£®∞¸∫¨-3∫Õ-4£©÷ƺ‰∂‘”¶µƒxµƒ»°÷µ∑∂Œßº¥ø…£ª
µƒ÷µ‘Ğ-3∫Õ-4£®∞¸∫¨-3∫Õ-4£©÷ƺ‰∂‘”¶µƒxµƒ»°÷µ∑∂Œßº¥ø…£ª
£®4£©œ»–¥≥ˆ∂˛¥Œ∫Ø ˝![]() πÿ”Ğ
πÿ”Ğ![]() µƒm∑÷∫Ø ˝y'£¨µ±x23x3£Ω1 ±£¨x£Ω1ªÚx£Ω4£¨µ±x2£´span>3x£´3£Ω1 ±£¨x£Ω
µƒm∑÷∫Ø ˝y'£¨µ±x23x3£Ω1 ±£¨x£Ω1ªÚx£Ω4£¨µ±x2£´span>3x£´3£Ω1 ±£¨x£Ω![]() ªÚx£Ω
ªÚx£Ω![]() £¨µ±y£Ωx23x3”Îœş∂ŒAB√ª”–Ωªµ„£¨m£º1£ªµ±y£Ωx23x3”Îœş∂ŒAB”–“ª∏ˆΩªµ„£¨y£Ωx2£´3x£´3”Îœş∂ŒAB”–“ª∏ˆΩªµ„£¨
£¨µ±y£Ωx23x3”Îœş∂ŒAB√ª”–Ωªµ„£¨m£º1£ªµ±y£Ωx23x3”Îœş∂ŒAB”–“ª∏ˆΩªµ„£¨y£Ωx2£´3x£´3”Îœş∂ŒAB”–“ª∏ˆΩªµ„£¨![]() £ºm£º
£ºm£º![]() £ªµ±y£Ωx23x3”Îœş∂ŒAB”–¡Ω∏ˆΩªµ„£¨m°ı4£Æ
£ªµ±y£Ωx23x3”Îœş∂ŒAB”–¡Ω∏ˆΩªµ„£¨m°ı4£Æ
£®1£©“ª¥Œ∫Ø ˝y£Ωx£´1µƒ2∑÷∫Ø ˝Œ™![]()
![]()
![]() ∞—
∞—![]() ¥˙»Î
¥˙»Î![]() µ√
µ√![]()
![]() £ª
£ª
£®2£©∑¥±»¿˝∫Ø ˝![]() µƒ4∑÷∫Ø ˝Œ™
µƒ4∑÷∫Ø ˝Œ™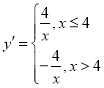 £¨
£¨
°‡yÀÊxµƒ‘ˆ¥Û∂¯º–° ±£¨![]() ªÚ
ªÚ![]() £ª
£ª
π ¥∞∏Œ™£∫![]() ªÚ
ªÚ![]() £ª
£ª
£®3£©∂˛¥Œ∫Ø ˝y£Ωx22x3πÿ”Ğxµƒ1∑÷∫Ø ˝Œ™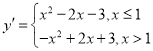
¢Ÿµ±1°İx°İ2 ±£¨
1°İx°İ1£¨y'=![]() £¨yµƒ»°÷µ∑∂ŒßŒ™4°İy'°İ0£¨
£¨yµƒ»°÷µ∑∂ŒßŒ™4°İy'°İ0£¨
1£ºx°İ2£¨y'=![]() £¨yµƒ»°÷µ∑∂ŒßŒ™3°İy'£º4£¨
£¨yµƒ»°÷µ∑∂ŒßŒ™3°İy'£º4£¨
°‡µ±1°İx°İ2 ±£¨y'µƒ»°÷µ∑∂ŒßŒ™4°İy'°İ0£¨3°İy'£º4£ª
¢Ğimg src="https://thumb.zyjl.cn/questionBank/Upload/2020/11/27/15/1b1ac277/SYS202011271558349761366940_DA/SYS202011271558349761366940_DA.033.png" width="15" height="13" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />∞—![]() ¥˙»Î
¥˙»Î![]() ø…µ√
ø…µ√![]()
∞—![]() ¥˙»Î
¥˙»Î![]() ø…µ√
ø…µ√![]()
![]() µ±
µ±![]() ±£¨
±£¨![]() µƒ»°÷µ∑∂ŒßŒ™
µƒ»°÷µ∑∂ŒßŒ™![]()
”…¢Ÿ÷™£¨µ±![]() ±£¨
±£¨![]()
∞—![]() ¥˙»Î
¥˙»Î![]() £¨Ω‚µ√£∫
£¨Ω‚µ√£∫![]() £¨
£¨![]() £®…·»•£©
£®…·»•£©
∞—![]() ¥˙»Î
¥˙»Î![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨![]() £®…·»•£©
£®…·»•£©
![]() kµƒ»°÷µ∑∂ŒßŒ™£∫
kµƒ»°÷µ∑∂ŒßŒ™£∫![]()
£®4£©∂˛¥Œ∫Ø ˝y£Ωx23x3µƒm∑÷∫Ø ˝Œ™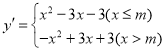
µ±x23x3£Ω1 ±£¨x£Ω1ªÚx£Ω4£¨
µ±x2£´3x£´3£Ω1 ±£¨x=![]() ªÚx£Ω
ªÚx£Ω![]() £¨
£¨
µ±y£Ωx23x3”Îœş∂ŒAB√ª”–Ωªµ„£¨m£º1£ª
µ±y£Ωx23x3”Îœş∂ŒAB”–“ª∏ˆΩªµ„£¨y£Ωx2£´3x£´3”Îœş∂ŒAB”–“ª∏ˆΩªµ„£¨
°‡![]() °İm£º
°İm£º![]() £ª
£ª
µ±y£Ωx23x3”Îœş∂ŒAB”–¡Ω∏ˆΩªµ„£¨m°ı4£ª
◊ğ…œÀ˘ ˆ£∫m£º1ªÚ![]() °İm£º
°İm£º![]() ªÚm°ı4£Æ
ªÚm°ı4£Æ

 øŒøŒ¡∑Ω≠À’œµ¡–¥∞∏
øŒøŒ¡∑Ω≠À’œµ¡–¥∞∏ √˚≈∆÷–—ßøŒ ±◊˜“µœµ¡–¥∞∏
√˚≈∆÷–—ßøŒ ±◊˜“µœµ¡–¥∞∏ √˜ÃÏΩÔ˝øŒ ±Ãÿ—µœµ¡–¥∞∏
√˜ÃÏΩÔ˝øŒ ±Ãÿ—µœµ¡–¥∞∏ ’„Ω≠–¬øŒ≥û˝Œ¨ƒø±Í≤‚∆¿øŒ ±Ãÿ—µœµ¡–¥∞∏
’„Ω≠–¬øŒ≥û˝Œ¨ƒø±Í≤‚∆¿øŒ ±Ãÿ—µœµ¡–¥∞∏