题目内容
⊙O的半径为1㎝,弦AB= ㎝,AC=
㎝,AC=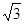 ㎝,则∠BAC的度数为 .
㎝,则∠BAC的度数为 .
15°或75°
解析试题分析:
延长AO,交圆于点D,那么AD就是圆O的直径.AD=2AO=2cm
连接BD,CD
∴∠DBA=∠DCA=90°
在三角形DBA中,AD=2cm,AB= cm,根据勾股定理得BD=
cm,根据勾股定理得BD= cm
cm
∴∠DAB=45°
在三角形DCA中,AD=2cm,AC= cm,根据勾股定理得CD=1cm
cm,根据勾股定理得CD=1cm
∴∠DAC=30°
根据题意,应有两种情况
①弦AB与弦AC在直径AD的同一侧
∴∠BAC=∠DAB-∠DAC=45°-30°=15°
②弦AB与弦AC在直径AD的两侧
∴∠BAC=∠DAB+∠DAC=45°+30°=75°
综上所述:∠BAC=75度或15度
考点:勾股定理、垂径定理、三角函数特殊值、直线与圆的位置关系
点评:难度中等,需要考虑会出现两种情况,这是考生的易错点。

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
⊙O的半径为5cm,弦AB∥CD,且AB=6cm,CD=8cm,则AB与CD之间的距离为( )
| A、1cm | B、7cm | C、3cm或4cm | D、1cm或7cm |
 如图,一种花边是由弓形组成的,
如图,一种花边是由弓形组成的, |
| ACB |
| A、2 | ||
B、
| ||
| C、3 | ||
D、
|
 如图,⊙O的半径为5,弦AB=8,OC⊥AB于C,则OC的长等于
如图,⊙O的半径为5,弦AB=8,OC⊥AB于C,则OC的长等于 如图,⊙O的半径为2,弦AB=
如图,⊙O的半径为2,弦AB=