Question

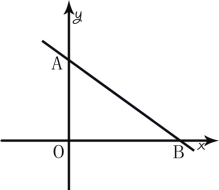
【题目】如图，直线MN与x轴、y轴分别相交于B、A两点，OA,OB的长满足式子

(1)求A，B两点的坐标;

(2)若点O到AB的距离为，求线段AB的长；

（3）在（2）的条件下，x轴上是否存在点P,使ΔABP使以AB为腰的等腰三角形，若存在请直接写出满足条件的点P的坐标.

Answer 1

【答案】 (1) A(0，6)B(8，0)；（2）；（3）存在，（-8,0）、（-2,0）、（18,0）.

【解析】

（1）根据非负数的性质可得OA=6、OB=8，即可求得A、B两点的坐标；（2）根据直角三角形面积的两种表示法即可求得AB的长；（3）分AB=B P1、AB=A P2、AB=B P3三种情况求点P的坐标.

（1）∵，

∴OA=6，OB=8，

∴A(0，6)，B(8，0)；

（2）∵，

∴AB=10；

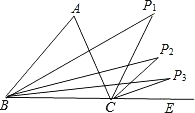
（3）在x轴上存在点P，是使ΔABP使以AB为腰的等腰三角形，点P的位置如图所示，

①当AB=BP1时，P1的坐标为（18，0）；②当AB=AP2时，P2的坐标为（-8，0）；③当AB=BP3时，P3的坐标为（-2，0）.