题目内容
6.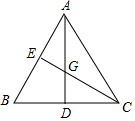 如图所示,在△ABC中,中线AD,CE交于点G,△ABC的面积为18cm2,求△AEG的面积.
如图所示,在△ABC中,中线AD,CE交于点G,△ABC的面积为18cm2,求△AEG的面积.
分析 根据三角形的中线把三角形分成面积相等的两个三角形求出△ACE的面积,再根据三角形的中线的交点到顶点的距离等于到对边中点的距离的2倍可得CG=2EG,然后根据等高的三角形的面积等于底边长的比列式进行计算即可得解.
解答 解:∵CE是△ABC的中线,
∴S△ACE=$\frac{1}{2}$S△ABC,
∵△ABC的中线AD与CE交于点G,
∴CG=2EG,
∴S△AEG=$\frac{1}{1+2}$S△ACE=$\frac{1}{3}$×$\frac{1}{2}$S△ABC=$\frac{1}{6}$S△ABC,
∵△ABC的面积为18cm2,
∴△AEG的面积=$\frac{1}{6}$×18=3cm2.
点评 本题考查了三角形的面积,主要利用了等底等高的三角形的面积相等的性质,熟记三角形的中线的交点到顶点的距离等于到对边中点的距离的2倍是解本题的关键.

练习册系列答案
相关题目
16.3$\frac{2}{7}$与(-2$\frac{5}{7}}$)的和是( )
| A. | $-\frac{3}{7}$ | B. | $1\frac{1}{7}$ | C. | $-\frac{3}{7}$ | D. | $\frac{4}{7}$ |
17.已知AB=6cm,C是AB的中点,那么AC为多长( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
16.方程4(a-x)-4(x+1)=60的解是x=1,则a的值为( )
| A. | -14 | B. | 20 | C. | 18 | D. | -16 |
 如图,已知AB∥CD,DF交AC于点E,交AB于点F,若E是AC的中点.求证:点E是DF的中点.
如图,已知AB∥CD,DF交AC于点E,交AB于点F,若E是AC的中点.求证:点E是DF的中点. 如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹)
如图是一名考古学家发现的一块古代车轮碎片,你能帮他找到这个车轮的半径吗?(画出示意图,保留作图痕迹)