题目内容
如图,已知双曲线 经过点M,它关于y轴对称的双曲线为
经过点M,它关于y轴对称的双曲线为 .
.
(1)求双曲线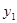 与
与 的解析式;
的解析式;
(2)若平行于 轴的直线交双曲线
轴的直线交双曲线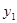 于点A,交双曲线
于点A,交双曲线 于点B,在
于点B,在 轴上存在点P,使以点A,B,O,P为顶点的四边形是菱形,求点P的坐标.
轴上存在点P,使以点A,B,O,P为顶点的四边形是菱形,求点P的坐标.
(1) ,
,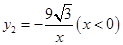 ;
;
(2)满足要求的点P有两个: 或
或 .
.
解析试题分析:(1)根据M点的坐标求出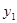 的解析式,根据对称性求出
的解析式,根据对称性求出 的解析式;
的解析式;
(2)设出A、B的坐标,根据四边形OPAB是菱形,得到 是等边三角形,求出AB,再利用勾股定理求出OE,OE等于点A的纵坐标,联立方程,从而求出P的坐标.
是等边三角形,求出AB,再利用勾股定理求出OE,OE等于点A的纵坐标,联立方程,从而求出P的坐标.
试题解析:(1) 在双曲线
在双曲线 上,
上,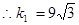 ,
, ,
, 双曲线
双曲线 与
与 关于
关于 轴对称,
轴对称,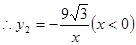 ;
;
(2) 双曲线
双曲线 与
与 关于
关于 轴对称
轴对称
∴点A与点B关于y轴对称,有OA=OB.
设 ,则
,则 ,AB=2m,
,AB=2m,
∵四边形OPAB是菱形,则OB=AB,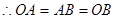 ,
, 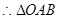 是等边三角形.
是等边三角形. ,
,  ,
, ,
,  .
. ,
,  ,
, 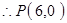 ,
,
同理,当四边形OABP是菱形时,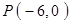
综上所述,满足要求的点P有两个: 或
或 .
.
考点:1.反比例函数2.菱形性质.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.

 的图象与反比例函数
的图象与反比例函数 的图象交于点
的图象交于点
 取何值时,反比例函数的值大于正比例函数的值?
取何值时,反比例函数的值大于正比例函数的值?
 (k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=
(k≠0)在第一象限内的图象经过点D,E,且tan∠BOA=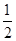 .
.
 的图象与反比例函数
的图象与反比例函数 的图象交于A、B两点,且点B的坐标为
的图象交于A、B两点,且点B的坐标为 .
.
 在反比例函数
在反比例函数
 (k为常数,且k≠0)的图像都经过点A(m,2).
(k为常数,且k≠0)的图像都经过点A(m,2).
 时,
时, 与
与 的大小。
的大小。
 在第一象限的图象如图所示,点A在其图象上,点B为
在第一象限的图象如图所示,点A在其图象上,点B为 轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB= .
轴正半轴上一点,连接AO、AB,且AO=AB,则S△AOB= .