Question

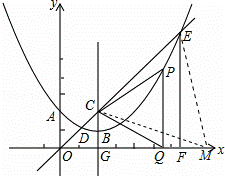
如图，在平面直角坐标系中，抛物线y=ax²+bx+c（a≠0）的顶点为B（2，1），且过点A（0，2），直线y=x与抛物线交于点D，E（点E在对称轴的右侧），抛物线的对称轴交直线y=x于点C，交x轴于点G，EF⊥x轴，垂足为F，点P在抛物线上，且位于对称轴的右侧，PQ⊥x轴，垂足为点Q，△PCQ为等边三角形

（1）求该抛物线的解析式；

（2）求点P的坐标；

（3）求证：CE=EF；

（4）连接PE，在x轴上点Q的右侧是否存在一点M，使△CQM与△CPE全等？若存在，试求出点M的坐标；若不存在，请说明理由．[注：3+2=（+1）²]．

Answer 1

解：（1）设抛物线的表达式为y=a（x﹣2）²+1，将点A（0，2）代入，得a（0﹣2）²+1=2，

解这个方程，得a=，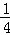

∴抛物线的表达式为y=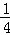（x﹣2）²+1=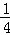x²﹣x+2；

（2）将x=2代入y=x，得y=2

∴点C的坐标为（2，2）即CG=2，

∵△PCQ为等边三角形

∴∠CQP=60°，CQ=PQ，

∵PQ⊥x轴，

∴∠CQG=30°，

∴CQ=4，GQ=2．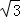

∴OQ=2+2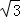，PQ=4，

将y=4代入y=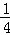（x﹣2）²+1，得4=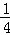（x﹣2）²+1

解这个方程，得x₁=2+2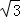=OQ，x₂=2﹣2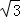＜0（不合题意，舍去）．

∴点P的坐标为（2+2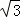，4）；

（3）把y=x代入y=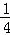x²﹣x+2，得x=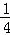x²﹣x+2

解这个方程，得x₁=4+2，x₂=4﹣2＜2（不合题意，舍去）

∴y=4+2=EF

∴点E的坐标为（4+2，4+2）

∴OE=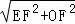=4+4，

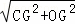又∵OC==2，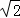

∴CE=OE﹣OC=4+2，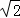

∴CE=EF；

（4）不存在．

如图，假设x轴上存在一点，使△CQM≌△CPE，则CM=CE，∠QCM=∠PCE

∵∠QCP=60°，

∴∠MCE=60°

又∵CE=EF，

∴EM=EF，

又∵点E为直线y=x上的点，

∴∠CEF=45°，

∴点M与点F不重合．

∵EF⊥x轴，这与“垂线段最短”矛盾，

∴原假设错误，满足条件的点M不存在．