题目内容
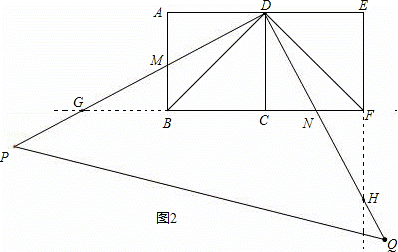
如图,两个边长均为2的正方形ABCD和正方形CDEF,点B、C、F在同一直线上,一直角三角板的直角顶点放置在D点处,DP交AB于点M,DQ交BF于点N.
(1)求证:△DBM≌△DFN;
(2)延长正方形的边CB和EF,分别与直角三角板的两边DP、DQ(或它们的延长线)交于点G和点H,试探究下列问题:
①线段BG与FH相等吗?说明理由;
②当线段FN的长是方程x2+2x﹣3=0的一根时,试求出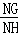 的值.
的值.

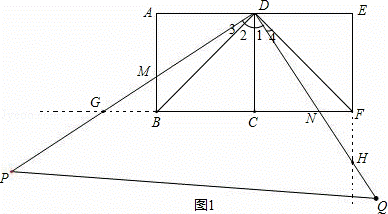
解:(1)如图1,∵四边形ABCD和四边形CDEF是边长正方形,
∴BC=FC,BD=FD,∠ABD=∠ADB=∠CDF=∠ADB=∠CFD=45°,∠DCB=∠DEF=∠E=∠HFN=∠ADC=90°.
∴∠ADM+∠CDM=90°,
∵∠PDQ=90°,
∴∠CDM+∠CDN=90°.
∴∠ADM=∠CDN.
∴∠ADB﹣∠ADM=∠CDF﹣∠CDN,
∴∠MDB=∠NDF.
在△DBM和△DFN中,
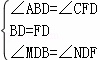 ,
,
∴△DBM≌△DFN(ASA);
(2)①四边形ABCD和四边形CDEF是边长正方形,
∴BC=FC=EF,BD=FD,∠ABD=∠ADB=∠CDF=∠ADB=∠CFD=45°,∠DCB=∠DEF=∠CDE=∠E=∠HFN=∠ADC=90°.
∴∠EDH+∠1=90°,
∵∠PDQ=90°,
∴∠CDM+∠1=90°.
∴∠CDM=∠EDH.
在△CDG和△EDH中,
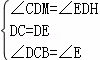 ,
,
∴△CDG≌△EDH(ASA),
∴CG=EH,
∴CG﹣CB=EH﹣EF,
∴BG=FH.
②∵x2+2x﹣3=0,
∴x1=1,x2=﹣3.
∵FN的长是方程x2+2x﹣3=0的一根,
∴FN=1.
∴CN=1,
∴CN=FN.
在△CND和△FNH中,
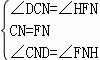 ,
,
∴△CND≌△FNH(ASA),
∴CD=FH=2,
∴GB=2,
∴GN=5.
在Rt△FNH中,由勾股定理,得NH=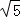 .
.
∴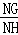 =
=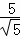 =
=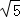 .
.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 的值是( )
的值是( ) B.
B.  C.
C.  D.
D. 
 (x>0)的图象经过顶点B,则k的值为__________.
(x>0)的图象经过顶点B,则k的值为__________.
 的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为1,则AC的长为__________(保留根号).
的图象在第一象限相交于点A,与x轴相交于点C,AB⊥x轴于点B,△AOB的面积为1,则AC的长为__________(保留根号).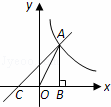
 有意义.
有意义.
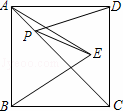
 D、AB运动至点D、B停止,动点P、Q从点C分别沿边CB、CD运动至点B、D停止,它们同时出发,设动点速度均为1cm/s,运动时间为t s,连接MN、NP、PQ、QM.
D、AB运动至点D、B停止,动点P、Q从点C分别沿边CB、CD运动至点B、D停止,它们同时出发,设动点速度均为1cm/s,运动时间为t s,连接MN、NP、PQ、QM.