题目内容
下列命题中是真命题的有（ ）个
①在1至50的50个整数中，有15个质数；
②若点C是线段AB上的一点，它把线段AB分割为两部分，使AC是AB与CB的比例中项，则我们把点C叫做线段AB的黄金分割点；
③方程2x2+3x=0两个根的积为-
；
④顶角为36°的等腰三角形叫做黄金三角形．
①在1至50的50个整数中，有15个质数；
②若点C是线段AB上的一点，它把线段AB分割为两部分，使AC是AB与CB的比例中项，则我们把点C叫做线段AB的黄金分割点；
③方程2x2+3x=0两个根的积为-
| 3 |
| 2 |
④顶角为36°的等腰三角形叫做黄金三角形．
| A、4 | B、3 | C、2 | D、1 |
考点：命题与定理
专题：
分析：利用质数的定义、黄金分割点、根与系数的关系及黄金三角形的定义分别判断后即可确定正确的选项．
解答：解：①在1至50的50个整数中，有15个质数，正确，为真命题；
②若点C是线段AB上的一点，它把线段AB分割为两部分，使AC是AB与CB的比例中项，则我们把点C叫做线段AB的黄金分割点，正确，为真命题；
③方程2x2+3x=0两个根的积为-
，错误，为假命题；
④顶角为36°的等腰三角形叫做黄金三角形，正确，为真命题．
故选B．
②若点C是线段AB上的一点，它把线段AB分割为两部分，使AC是AB与CB的比例中项，则我们把点C叫做线段AB的黄金分割点，正确，为真命题；
③方程2x2+3x=0两个根的积为-
| 3 |
| 2 |
④顶角为36°的等腰三角形叫做黄金三角形，正确，为真命题．
故选B．
点评：本题考查了质数的定义、黄金分割点、根与系数的关系及黄金三角形的定义，属于基础定义，比较简单．
练习册系列答案
相关题目
如图，下列说法中错误的是（ ）| A、OA的方向是东北方向 |
| B、OB的方向是北偏西30° |
| C、OC的方向是南偏西60° |
| D、OD的方向是南偏东30° |
将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上，点A、B的读数分别为88°，30°，则∠ACB的度数为下列四个命题：①三个角都相等的三角形是等边三角形；②有两个角等于60°的三角形是等边三角形；③有一个角时60°的等腰三角形是等边三角形；④两个角相等的等腰三角形是等边三角形，其中，假命题有（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
当k＜0，b＜0时，函数y=kx+b的图象大致是（ ）
A、 |
B、 |
C、 |
D、 |
以下等式变形不正确的是（ ）
| A、由x=y，得到x+2=y+2 |
| B、由2a-3=b-3，得到2a=b |
| C、由m=n，得到2am=2an |
| D、由am=an，得到m=n |
已知函数y=（m2+m）x2+mx+4为二次函数，则m的取值范围是（ ）
| A、m≠0 |
| B、m≠-1 |
| C、m≠0，且m≠-1 |
| D、m=-1 |
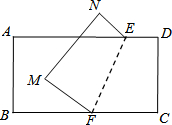如图，将一张长方形的纸片沿折痕E、F翻折，使点C、D分别落在点M、N的位置，且∠BFM=| 1 |
| 2 |
| A、30° | B、36° |
| C、45° | D、60° |