题目内容
3.先化简,再求值:$\frac{{x}^{2}-4xy+4{y}^{2}}{{x}^{2}-3xy}$÷($\frac{-5{y}^{2}}{x-3y}$-x-3y)+$\frac{1}{x}$,其中x、y满足(x-1)2+|y-2|=0.分析 原式第一项括号中两项通分并利用同分母分式的减法法则计算,再利用除法法则变形,约分后两项通分并利用同分母分式的加法法则计算得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.
解答 解:原式=$\frac{(x-2y)^{2}}{x(x-3y)}$÷$\frac{-5{y}^{2}-(x+3y)(x-3y)}{x-3y}$+$\frac{1}{x}$=$\frac{(x-2y)^{2}}{x(x-3y)}$•$\frac{x-3y}{(2y+x)(2y-x)}$+$\frac{1}{x}$=$\frac{2y-x}{x(2y+x)}$+$\frac{1}{x}$=$\frac{2y-x+2y+x}{x(2y+x)}$=$\frac{4y}{x(x+2y)}$,
∵(x-1)2+|y-2|=0,
∴x=1,y=2,
则 原式=$\frac{8}{5}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.有四张不透明的卡片,正面分别标有数字3、$\frac{25}{9}$、$\sqrt{3}$、π.除正面的数字不同外,其余都相同.将它们背面朝上洗匀后,从中随机抽取一张,抽到写有无理数卡片的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
18.融侨半岛某文具店购入一批笔袋进行销售,进价为每个20元,当售价为每个50元时,每星期可以卖出100个,现需降价处理:售价每降价3元,每星期可以多卖出15个,店里每星期笔袋的利润要达到3125元.若设店主把每个笔袋售价降低x元,则可列方程为( )
| A. | (30+x)(100-15x)=3125 | B. | (30-x)(100+15x)=3125 | ||
| C. | (30+x)(100-5x)=3125 | D. | (30-x)(100+5x)=3125 |
12.$\frac{3}{4}$的相反数是( )
| A. | -1$\frac{1}{3}$ | B. | -|-$\frac{3}{4}$| | C. | -(-1$\frac{1}{3}$) | D. | |-$\frac{3}{4}$| |
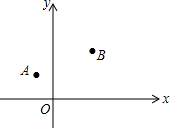 如图所示,x轴所在直线是一条东西走向的河,A(-2,3)、B(4,5)两个村庄位于河的北岸,现准备在河上修建一净水站P,并利用管道为两个村庄供水(单位:千米).
如图所示,x轴所在直线是一条东西走向的河,A(-2,3)、B(4,5)两个村庄位于河的北岸,现准备在河上修建一净水站P,并利用管道为两个村庄供水(单位:千米).