Question

14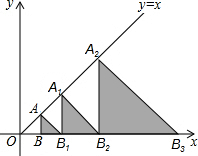．如图，点A，A₁，A₂，…都在直线y=x上，点B，B₁，B₂，B₃，…都在x轴上，且△ABB₁，△A₁B₁B₂，△A₂B₂B₃，…都是等腰直角三角形，若按如此规律排列下去，已知B（1，0），则A₂₀₁₆的坐标为（2²⁰¹⁶，2²⁰¹⁶）．

Answer 1

分析 根据规律得出OB₁=2，OB₂=4，OB₃=8，OB₄=16，OB₅=32，所以可得OB_n=2ⁿ，再由等腰直角三角形的性质可得A_nB_n=OB_n，进而解答即可．

解答 解：∵△ABO，△AB₁B，…，△A_nB_nB_n+1都是等腰直角三角形，
∵OB=1，∴AB=1，
∴OB₂=2，
进而得出OB₃=8，OB₄=16，OB₅=16，
∴OB_n=2ⁿ，
∴OB₂₀₁₆=2²⁰¹⁶，
∴A_nB_n=OB_n=2²⁰¹⁶，
即点A₂₀₁₆的坐标为（2²⁰¹⁶，2²⁰¹⁶），
故答案为：（2²⁰¹⁶，2²⁰¹⁶）．

点评 此题考查一次函数图象上点的坐标特征，等腰直角三角形的性质，关键是根据规律得出OB_n=2ⁿ进行解答．