题目内容
8.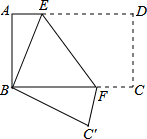 如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C'处,折痕为EF,若AB=1,BC=2,则△ABE和△BC'F的周长之和是6.
如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C'处,折痕为EF,若AB=1,BC=2,则△ABE和△BC'F的周长之和是6.
分析 根据翻折变换的性质可得BE=ED,BC′=CD,C′F=CF,然后求出两个三角形的周长的和等于矩形的周长,再求解即可.
解答 解:∵矩形纸片ABCD折叠,点D与点B重合,点C落在C'处,
∴BE=ED,BC′=CD,C′F=CF,
∴△ABE的周长=AB+AE+BE=AB+AE+ED=AB+AD,
△BC′F的周长=BF+C′F+BC′=BE+CF+CD=BC+CD,
∴△ABE和△BC′F的周长之和=AB+AD+BC+CD=矩形ABCD的周长,
∵AB=1,BC=2,
∴△ABE和△BC′F的周长之和=2×(1+2)=2×3=6.
故答案为:6.
点评 本题考查了翻折变换的性质,矩形的性质,翻折的问题,要准确确定出翻折前后相等的对应边.

练习册系列答案
相关题目
19. 如图,AP为⊙O的切线,P为切点,若∠A=30°,C、D为圆周上两点,且∠PDC=70°,则∠OBC等于( )
如图,AP为⊙O的切线,P为切点,若∠A=30°,C、D为圆周上两点,且∠PDC=70°,则∠OBC等于( )
 如图,AP为⊙O的切线,P为切点,若∠A=30°,C、D为圆周上两点,且∠PDC=70°,则∠OBC等于( )
如图,AP为⊙O的切线,P为切点,若∠A=30°,C、D为圆周上两点,且∠PDC=70°,则∠OBC等于( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
16.计算:($\frac{1}{1-x}$-$\frac{1}{x+1}$)÷$\frac{x}{x-1}$=( )
| A. | $\frac{2}{x+1}$ | B. | $\frac{2}{x-1}$ | C. | -$\frac{2}{x+1}$ | D. | -$\frac{2}{x-1}$ |
3.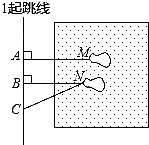 如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )
如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )
 如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )
如图是某同学在体育课上跳远后留下的脚印,那么他的跳远成绩可以用图中哪条线段的长度表示( )| A. | 线段AM | B. | 线段BN | C. | 线段CN | D. | 无法确定 |
13.若一次函数y=(k-1)x+3的图象经过第一、二、四象限,则k的取值范围是( )
| A. | k>0 | B. | k<0 | C. | k>1 | D. | k<1 |
18. 如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )
如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )
 如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )
如图,在边长为2的菱形ABCD中,∠A=60°,DE⊥AB,DF⊥BC,则△DEF的周长为( )| A. | 3 | B. | $\sqrt{3}$ | C. | 6 | D. | $3\sqrt{3}$ |
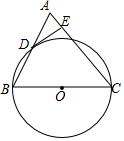 如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.
如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.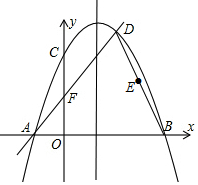 已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).
已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).