��Ŀ����
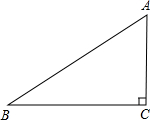
��ͼ����֪����ABCD�У�AD��BC��AD=2��AB=BC=8��CD=10��
��1��������ABCD�����S��
��2������P�ӵ�B��������1cm/s���ٶȣ���B?A?D?C�������C�˶�������Q�ӵ�C��������1cm/s���ٶȣ���C?D?A�������A�˶�������Q��QE��BC�ڵ�E����P��Q����ͬʱ������������һ�㵽��Ŀ�ĵ�ʱ�����˶���֮���������˶�ʱ��Ϊt�룮�ʣ�
�ٵ���P��B?A���˶�ʱ���Ƿ����������t��ʹ��ֱ��PQ������ABCD���ܳ�ƽ�֣������ڣ������t��ֵ���������ڣ���˵�����ɣ�
�����˶������У��Ƿ����������t��ʹ����P��A��DΪ��������������CQE���ƣ������ڣ���������з���������t��ֵ���������ڣ���˵�����ɣ�
�����˶������У��Ƿ����������t��ʹ����P��D��QΪ�����������ǡ������DQΪһ���ĵ��������Σ������ڣ���������з���������t��ֵ���������ڣ���˵�����ɣ�
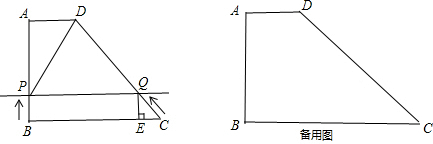
��1��������ABCD�����S��
��2������P�ӵ�B��������1cm/s���ٶȣ���B?A?D?C�������C�˶�������Q�ӵ�C��������1cm/s���ٶȣ���C?D?A�������A�˶�������Q��QE��BC�ڵ�E����P��Q����ͬʱ������������һ�㵽��Ŀ�ĵ�ʱ�����˶���֮���������˶�ʱ��Ϊt�룮�ʣ�
�ٵ���P��B?A���˶�ʱ���Ƿ����������t��ʹ��ֱ��PQ������ABCD���ܳ�ƽ�֣������ڣ������t��ֵ���������ڣ���˵�����ɣ�
�����˶������У��Ƿ����������t��ʹ����P��A��DΪ��������������CQE���ƣ������ڣ���������з���������t��ֵ���������ڣ���˵�����ɣ�
�����˶������У��Ƿ����������t��ʹ����P��D��QΪ�����������ǡ������DQΪһ���ĵ��������Σ������ڣ���������з���������t��ֵ���������ڣ���˵�����ɣ�

��1����D��DH��AB��BC��H�㣬
��AD��BH��DH��AB��
���ı���ABHD��ƽ���ı��Σ�
��DH=AB=8��BH=AD=2��
��CH=8-2=6��
��CD=10��
��DH2+CH2=CD2���DHC=90�㣮
��B=��DHC=90�㣮
������ABCD��ֱ�����Σ�
��SABCD=
��AD+BC��AB=
����2+8����8=40��
��2���١�BP=CQ=t��
��AP=8-t��DQ=10-t��
��AP+AD+DQ=PB+BC+CQ��
��8-t+2+10-t=t+8+t��
��t=3��8��
�൱t=3��ʱ��PQ������ABCD�ܳ�ƽ�֣�
�ڵ�һ�������0��t��8����PAD����QEC���ADP=��C
��tan��ADP=tan��C=
=
��
=
����t=
����PAD����CEQ���APD=��C
��tan��APD=tan��C=
=
����
=
��t=
�ڶ��������8��t��10��P��A��D���㲻����������Σ�
�����������10��t��12��ADPΪ�۽���������Rt��CQE�����ƣ�
��t=
��t=
ʱ����PAD���CQE���ƣ�
�۵�һ���������0��t��8ʱ����Q����QE��BC��QH��AB������ΪE��H��
��AP=8-t��AD=2��
��PD=
=
��
��CE=
t��QE=
t��
��QH=BE=8-
t��BH=QE=
t��
��PH=t-
t=
t��
��PQ=
=
��DQ=10-t��
��DQ=DP��10-t=
��
���t=8�룮
��DQ=PQ��10-t=
��
����ã�3t2-52t+180=0
��ã�t=
��t=
��8������������ȥ��
��t=
�ڶ��������8��t��10ʱ��DP=DQ=10-t��
�൱8��t��10ʱ����DQΪ���ĵ�����DPQ�������
�����������10��t��12ʱ��DP=DQ=t-10��
�൱10��t��12ʱ����DQΪ���ĵ�����DPQ�������
����������t=
��8��t��10��10��t��12ʱ����DQΪ���ĵ�����DPQ������

��AD��BH��DH��AB��
���ı���ABHD��ƽ���ı��Σ�
��DH=AB=8��BH=AD=2��
��CH=8-2=6��
��CD=10��
��DH2+CH2=CD2���DHC=90�㣮
��B=��DHC=90�㣮
������ABCD��ֱ�����Σ�
��SABCD=
| 1 |
| 2 |
| 1 |
| 2 |
��2���١�BP=CQ=t��
��AP=8-t��DQ=10-t��
��AP+AD+DQ=PB+BC+CQ��
��8-t+2+10-t=t+8+t��
��t=3��8��
�൱t=3��ʱ��PQ������ABCD�ܳ�ƽ�֣�
�ڵ�һ�������0��t��8����PAD����QEC���ADP=��C

��tan��ADP=tan��C=
| 8 |
| 6 |
| 4 |
| 3 |
��
| 8-t |
| 2 |
| 4 |
| 3 |
| 16 |
| 3 |
����PAD����CEQ���APD=��C
��tan��APD=tan��C=
| 8 |
| 6 |
| 4 |
| 3 |
| 2 |
| 8-t |
| 4 |
| 3 |
��t=
| 13 |
| 2 |
�ڶ��������8��t��10��P��A��D���㲻����������Σ�
�����������10��t��12��ADPΪ�۽���������Rt��CQE�����ƣ�
��t=
| 16 |
| 3 |
| 13 |
| 2 |

�۵�һ���������0��t��8ʱ����Q����QE��BC��QH��AB������ΪE��H��
��AP=8-t��AD=2��
��PD=
| AP2+AD2 |
| t2-16t+68 |
��CE=
| 3 |
| 5 |
| 4 |
| 5 |
��QH=BE=8-
| 3 |
| 5 |
| 4 |
| 5 |
��PH=t-
| 4 |
| 5 |
| 1 |
| 5 |
��PQ=
| QH2+PH2 |
|

��DQ=DP��10-t=
| t2-16t+68 |
���t=8�룮
��DQ=PQ��10-t=
|
����ã�3t2-52t+180=0
��ã�t=
26-2
| ||
| 3 |
26+2
| ||
| 3 |
��t=
26-2
| ||
| 3 |
�ڶ��������8��t��10ʱ��DP=DQ=10-t��
�൱8��t��10ʱ����DQΪ���ĵ�����DPQ�������
�����������10��t��12ʱ��DP=DQ=t-10��
�൱10��t��12ʱ����DQΪ���ĵ�����DPQ�������
����������t=
26-2
| ||
| 3 |



��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 +6m=0������ʵ������
+6m=0������ʵ������