题目内容
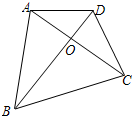
如图,四边形ABCD的对角线AC与BD相交于点O,∠ADO=∠BCO
求证:△ABO∽△DCO.
求证:△ABO∽△DCO.

证明:∵∠ADO=∠BCO,∠AOD=∠BOC,
∴△AOD∽△BOC,
∴
=
,
∴
=
,
又∵∠AOB=∠DOC,
∴△ABO∽△DCO.
∴△AOD∽△BOC,
∴
| OA |
| OB |
| OD |
| OC |
∴
| OA |
| OD |
| OB |
| OC |
又∵∠AOB=∠DOC,
∴△ABO∽△DCO.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目