Question

1．如图，在?ABCD中，E为边BC的中点，F为线段AE上一点，联结BF并延长交边AD于点G，过点G作AE的平行线，交射线DC于点H．设$\frac{AD}{AB}$=$\frac{EF}{AF}$=x．
（1）当x=1时，求AG：AB的值；
（2）设$\frac{{S}_{△GDH}}{{S}_{△EBA}}$=y，求关于x的函数关系式，并写出x的取值范围；
（3）当DH=3HC时，求x的值．

Answer 1

分析 （1）由平行四边形ABCD，得到AD与BC平行且相等，由两直线平行得到两对内错角相等，进而确定出三角形BEF与三角形AGF相似，由相似得比例，把x=1代入已知等式，结合比例式得到AG=BE，AD=AB，即可求出所求式子的值；
（2）设AB=1，根据已知等式表示出AD与BE，由AD与BC平行，得到比例式，表示出AG与DG，利用两角相等的三角形相似得到三角形GDH与三角形ABE相似，利用相似三角形面积之比等于相似比的平方列出y与x的函数解析式，并求出x的范围即可；
（3）分两种情况考虑：①当点H在边DC上时，如图1所示；②当H在DC的延长线上时，如图2所示，分别利用相似得比例列出关于x的方程，求出方程的解即可得到x的值．

解答 解：（1）在?ABCD中，AD=BC，AD∥BC，
∴∠BEF=∠GAF，∠EBF=∠AGF，
∴△BEF∽△GAF，
∴$\frac{BE}{AG}$=$\frac{EF}{AF}$，
∵x=1，即$\frac{AD}{AB}$=$\frac{EF}{AF}$=1，
∴$\frac{AD}{AB}$=$\frac{BE}{AG}$=1，
∴AD=AB，AG=BE，
∵E为BC的中点，
∴BE=$\frac{1}{2}$BC，
∴AG=$\frac{1}{2}$AB，
则AG：AB=$\frac{1}{2}$；
（2）∵$\frac{AD}{AB}$=$\frac{EF}{AF}$=x，
∴不妨设AB=1，则AD=x，BE=$\frac{1}{2}$x，
∵AD∥BC，
∴$\frac{BE}{AG}$=$\frac{EF}{AF}$=x，
∴AG=$\frac{1}{2}$，DG=x-$\frac{1}{2}$，
∵GH∥AE，
∴∠DGH=∠DAE，
∵AD∥BC，
∴∠DAE=∠AEB，
∴∠DGH=∠AEB，
在?ABCD中，∠D=∠ABE，
∴△GDH∽△EBA，
∴$\frac{{S}_{△GDH}}{{S}_{△EBA}}$=（$\frac{DG}{BE}$）²，
∴y=（$\frac{x-\frac{1}{2}}{\frac{1}{2}x}$）²=$\frac{4{x}^{2}-4x+1}{{x}^{2}}$（x＞$\frac{1}{2}$）；
（3）分两种情况考虑：
①当点H在边DC上时，如图1所示：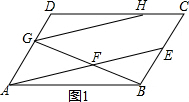

∵DH=3HC，
∴$\frac{DH}{DC}$=$\frac{3}{4}$，
∴$\frac{DH}{AB}$=$\frac{3}{4}$，
∵△GDH∽△EBA，
∴$\frac{DG}{BE}$=$\frac{DH}{AB}$=$\frac{3}{4}$，即$\frac{x-\frac{1}{2}}{\frac{1}{2}x}$=$\frac{3}{4}$，
解得：x=$\frac{4}{5}$；
②当H在DC的延长线上时，如图2所示：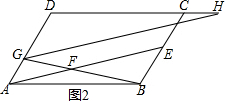

∵DH=3HC，
∴$\frac{DH}{DC}$=$\frac{3}{2}$，
∴$\frac{DH}{AB}$=$\frac{3}{2}$，
∵△GDH∽△EBA，
∴$\frac{DG}{BE}$=$\frac{DH}{AB}$=$\frac{3}{2}$，即$\frac{x-\frac{1}{2}}{\frac{1}{2}x}$=$\frac{3}{2}$，
解得：x=2，
综上所述，可知x的值为$\frac{4}{5}$或2．

点评 此题属于相似型综合题，涉及的知识有：平行四边形的性质，相似三角形的判定与性质，以及平行线的性质，熟练掌握相似三角形的判定与性质是解本题的关键．