题目内容
已知正比例函数y=（a+3）x（a＜0）与反比例函数
的图象有两个公共点，其中一个公共点的纵坐标为4．
（1）求这两个函数的解析式；
（2）在坐标系中画出它们的图象（可不列表）．
解：（1）将y=4代入两函数解析式得，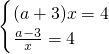
，
原式可化为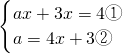
，
②代入①得，2x2+3x-2=0，
解得x1=-2，x2=
，
代入②得，a1=-5，a2=5．
由于a＜0，故取a=-5．
所以两函数解析式为y=-2x和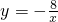
．
（2）
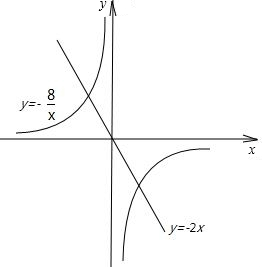
分析：（1）因为两函数一个公共点的纵坐标为4，所以可把4代入正比例函数y=（a+3）x（a＜0）与反比例函数得到关于a、x的方程组，求出a的值，进而可求出两函数的解析式；
（2）在正比例函数y=-2x上分别令x=1、x=2求出y的对应值，描出此两点即可画出此函数的图象；
点评：此题考查了反比例函数与一次函数的交点问题，将函数图象的交点与方程组的解结合起来是解此类题目常用的方法．
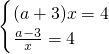，原式可化为
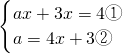，②代入①得，2x2+3x-2=0，
解得x1=-2，x2=
，代入②得，a1=-5，a2=5．
由于a＜0，故取a=-5．
所以两函数解析式为y=-2x和
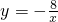．（2）
分析：（1）因为两函数一个公共点的纵坐标为4，所以可把4代入正比例函数y=（a+3）x（a＜0）与反比例函数
得到关于a、x的方程组，求出a的值，进而可求出两函数的解析式；（2）在正比例函数y=-2x上分别令x=1、x=2求出y的对应值，描出此两点即可画出此函数的图象；
点评：此题考查了反比例函数与一次函数的交点问题，将函数图象的交点与方程组的解结合起来是解此类题目常用的方法．
练习册系列答案
相关题目
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为（-2，-1），则它的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
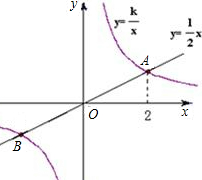横坐标为2．
如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．