题目内容
如图,AB经过⊙O上的点C,且OA=OB,CA=CB,⊙O分别与OA、OB的交点D、E恰好是OA、OB的中点,EF切⊙O于点E,交AB于点F.
 (1)求证:AB是⊙O的切线;
(1)求证:AB是⊙O的切线;
(2)若∠A=30°,⊙O的半径为2,求DF的长.
(1)证明:连结OC,
∵OA=OB,CA=CB,
∴OC⊥AB.
∵OC是半径,
∴AB是⊙O的切线.
(2)解:过点D作DM⊥AB于点M,
∵D、E分别是OA、OB的中点,⊙O的半径为2,
 ∴OD=OE=AD=BE=2.
∴OD=OE=AD=BE=2.
∵OA=OB,∠A=30°,
∴∠B=∠A =30°.
∵EF切⊙O于点E,
∴EF⊥OE.
∴∠BEF =90°.
∴ ,
, .
.
在Rt 中,∠A =30°,AD=2,
中,∠A =30°,AD=2,
∴DM=1, .
.
在Rt 中,∠A =30°,OA=4,
中,∠A =30°,OA=4,
∴ .
. .
.
∴ .
.
在Rt 中,
中, .… 5分
.… 5分

练习册系列答案
相关题目
 的绝对值是
的绝对值是 B.
B.  C.
C. 
 的值为零,则
的值为零,则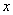 的值为 .
的值为 . ,求
,求 的值.
的值. 的绝对值是
的绝对值是 B. 3 C.
B. 3 C. 
 ,线段BC的长为
,线段BC的长为 ,则下列图象中,能表示
,则下列图象中,能表示




 的坐标为(
的坐标为( ,
, )(其中k为常数,且
)(其中k为常数,且 ),则称点
),则称点 ,
, ),即
),即 为等腰直角三角形,则k的值为____________;
为等腰直角三角形,则k的值为____________; ),点A在函数
),点A在函数 (
( )的图象上,且点A是点B的“
)的图象上,且点A是点B的“ 属派生点”,当线段B Q最短时,求B点坐标.
属派生点”,当线段B Q最短时,求B点坐标.
