题目内容
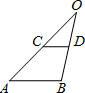如图，在△OAB中，CD∥AB，若OC：OA=1：2，则下列结论：
（1）
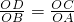；（2）AB=2CD；（3）S△OAB=2S△OCD．
其中正确的结论是
- A.（1）（2）
- B.（1）（3）
- C.（2）（3）
- D.（1）（2）（3）
A
分析：根据AB∥CD可得△ABO∽△DOC，即可得=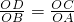
=
，根据相似三角形面积的比等于相似比的平方，可得S△OCD=4S△OAB，即可判断各结论的正误．
解答：∵AB∥CD，
∴△ABO∽△DOC，
∴==，
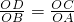∴AB=2CD，
∴4S△OCD=S△OAB（相似三角形面积的比等于相似比的平方）．
故结论（1）（2）正确．
故选A．
点评：本题考查了平行线的性质及平分线段成比例的性质，涉及到相似三角形的判定及性质，是一道小综合题．
分析：根据AB∥CD可得△ABO∽△DOC，即可得
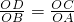==，根据相似三角形面积的比等于相似比的平方，可得S△OCD=4S△OAB，即可判断各结论的正误．解答：∵AB∥CD，
∴△ABO∽△DOC，
∴
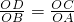==，∴AB=2CD，
∴4S△OCD=S△OAB（相似三角形面积的比等于相似比的平方）．
故结论（1）（2）正确．
故选A．
点评：本题考查了平行线的性质及平分线段成比例的性质，涉及到相似三角形的判定及性质，是一道小综合题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
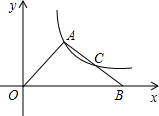（2012•泸州）如图，在△OAB中，C是AB的中点，反比例函数y=
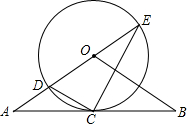如图，在△OAB中，OA=OB，以点O为圆心的⊙0经过AB的中点C，直线AO与⊙0相交于点D、E，连接CD、CE．
如图，在△OAB中，C是AB的中点，反比例函数y=
如图，在△OAB中，∠B=90°，∠BOA=30°，OA=4，将△OAB绕点O按逆时针方向旋转至△OA′B′，C点的坐标为（0，4）．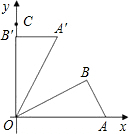
（创新学习）如图，在△OAB中，∠B=90°，∠BOA=30°，OA=4，将△OAB绕点O按逆时针方向旋转至△OA′B′，C点的坐标为（0，4）．