Question

15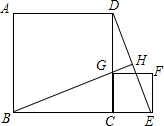．如图，正方形ABCD边长为1，G为CD边上的一个动点（点G与C、D不重合），以CG为一边向正方形ABCD外作正方形GCEF，连接DE交BG的延长线于点H．
（1）求证：BH⊥DE；
（2）当BH垂直平分DE时，求CG的长度？请说明理由．（提示：要有辅助线哟？）

Answer 1

分析 （1）先由四边形ABCD和CGFE是正方形求证△DCE≌△BCG，再得出BG⊥DE．
（2）连接BD，解题关键是利用垂直平分线的性质得出BD=BE，从而找到BD=$\sqrt{2}$，CE=BE-BC=$\sqrt{2}$-1，根据全等三角形的性质求解即可．

解答 （1）证明：
∵正方形ABCD，
∴∠BCD=90°，BC=CD，
同理：CG=CE，
∠GCE=90°，
∴∠BCD=∠GCE=90°，
$\left\{\begin{array}{l}{BC=CD}\\{∠BCD=∠GCE=90°}\\{CG=CE}\end{array}\right.$，
∴△BCG≌△DCE，
∴∠GBC=∠CDE，
在Rt△DCE中∠CDE+∠CED=90°，
∴∠GBC+∠BEH=90°，
∴∠BHE=180°-（∠GBC+∠BHE）=90°，
∴BH⊥DE；
（2）当CG=$\sqrt{2}$-1时BH垂直平分DE，
理由如下：
若BH垂直平分DE，连接BD，
∴BD=BE，
∵BD=$\sqrt{2}$
∴CG=CE=BE-BC=$\sqrt{2}$-1．

点评 此题主要考查正方形的性质，全等三角形的判定和线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段的两个端点的距离相等．特殊图形的特殊性质要熟练掌握．