题目内容
14.在一个不透明的袋中有6个除颜色外其它都相同的小球,其中3个红球,2个黄球,1个白球.①小明从中任意摸出一个小球,摸到的白球机会是$\frac{1}{6}$;
②小明和小亮商定一个游戏,规则如下:小明从中任意摸出一个小球,摸到红球则小明胜,否则小亮胜,问该游戏对双方是否公平,为什么?
分析 ①由题意可得,共有6种等可能的结果,其中从口袋中任意摸出一个球是白球的有1种情况,利用概率公式即可求得答案;
②游戏公平,分别计算他们各自获胜的概率即可.
解答 解:①∵在一个不透明的口袋中有6个除颜色外其余都相同的小球,其中3个红球,2个黄球,1个白球,
∴从口袋中任意摸出一个球是白球的概率=$\frac{1}{6}$,
故答案为$\frac{1}{6}$;
②该游戏对双方是公平的,理由如下:
由题意可知小明获胜的概率=$\frac{3}{6}$=$\frac{1}{2}$,小亮获胜的概率=$\frac{2+1}{6}$=$\frac{1}{2}$,
所以他们获胜的概率相等,
即游戏是公平的.
点评 此题考查了概率公式的应用.此题比较简单,注意概率=所求情况数与总情况数之比.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
2.下列长度的各组线段能组成三角形的是( )
| A. | 3cm、8cm、5cm | B. | 15cm、10cm、7cm | C. | 5cm、5cm、10cm | D. | 12cm、5cm、6cm |
19.△ABC中,∠A=55°,∠B=60°,则∠C=( )
| A. | 50° | B. | 60° | C. | 70° | D. | 65° |
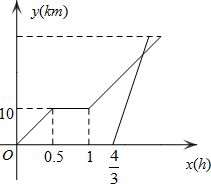 周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后达到甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同的路线前往乙地,他们离家的路程y(km)与小明离家时间x(h)之间的关系如图所示,已知妈妈驾车的速度是小明汽车速度的3倍
周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后达到甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同的路线前往乙地,他们离家的路程y(km)与小明离家时间x(h)之间的关系如图所示,已知妈妈驾车的速度是小明汽车速度的3倍