题目内容
8.已知(4x-2y-1)2+$\sqrt{xy-2}$=0,求4x2y-4x2y2+xy2的值.分析 根据非负数的性质列方程组求出x、y,原式提取公因式后代入计算即可求出值.
解答 解:∵(4x-2y-1)2+$\sqrt{xy-2}$=0,
∴$\left\{\begin{array}{l}{4x-2y=1}\\{xy=2}\end{array}\right.$,
消去y得:x(2x-$\frac{1}{2}$)=2,即4x2-x-4=0,
解得:x=$\frac{1±\sqrt{65}}{8}$,
把x=$\frac{1±\sqrt{65}}{8}$代入得:y=$\frac{-1±\sqrt{65}}{4}$,
则原式=xy(4x-4xy+y)=2(1+3y-8)=-14+6y=$\frac{-31±\sqrt{65}}{2}$.
点评 此题考查了提公因式法与公式法的综合运用,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.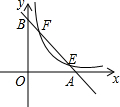 如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
 如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )
如图,已知直线y=-x+3分别与x轴,y轴交于A,B两点,与双曲线y=$\frac{k}{x}$交于E,F两点.若AB=3EF,则k的值是( )| A. | $\frac{\sqrt{6}}{2}$ | B. | 2 | C. | $\frac{5}{4}$ | D. | $\frac{3}{4}$ |
3.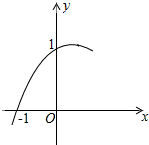 如图是二次函数y=ax2+bx+c是图象的一部分,记M=a+b,则M的取值范围是( )
如图是二次函数y=ax2+bx+c是图象的一部分,记M=a+b,则M的取值范围是( )
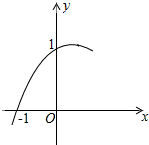 如图是二次函数y=ax2+bx+c是图象的一部分,记M=a+b,则M的取值范围是( )
如图是二次函数y=ax2+bx+c是图象的一部分,记M=a+b,则M的取值范围是( )| A. | -1<M<0 | B. | -1<M<1 | C. | 0<M<1 | D. | 不能确定 |
13.关于x的两个多项式乘积:(x+a)(x+b)的结果是( )
| A. | x2-ab | B. | x2+ab | C. | x2+(a-b)x+ab | D. | x2+(a+b)x+ab |
 如图,直线AB和CD相交于点O,FO⊥CD于点O,∠1=∠3,试判断EO与AB有何特殊位置关系,并说明理由.
如图,直线AB和CD相交于点O,FO⊥CD于点O,∠1=∠3,试判断EO与AB有何特殊位置关系,并说明理由.