题目内容
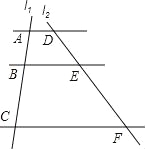
如图,AD∥BE∥CF,直线l1,l2与三条平行线分别交于点A,B,C和点D,E,F.若AC=3,BC=2,DE=1.5,则DF的长为 .
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
题目内容
如图,AD∥BE∥CF,直线l1,l2与三条平行线分别交于点A,B,C和点D,E,F.若AC=3,BC=2,DE=1.5,则DF的长为 .

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案