题目内容
如图所示．已知P为△ABC内一点，AP，BP，CP分别与对边交于D，E，F，把△ABC分成六个小三角形，其中四个小三角形的面积已在图中给出．求△ABC的面积．
解：设S△APE=x，S△BPF=y，
∵S△BDP=40，S△CDP=30，S△CEP=35，
∴
=
=
，
∴
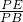=①，
同理可得
=
②，
解关于①②的方程组，得
，
故S△ABC=40+30+35+70+84+56=315．
分析：先设S△APE=x，S△BPF=y，根据同高不同底的两个三角形的面积比等于它们的底之比，可得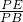==，从而有=①，同理可得=②，解①②组成的方程组，而S△ABC=S△BDP+S△CDP+S△CPE+S△APE+S△APF+S△BPF，易求其面积．
点评：本题考查了三角形面积、解二元一次方程组．注意：同高不同底的两个三角形的面积比等于它们的底之比．
∵S△BDP=40，S△CDP=30，S△CEP=35，
∴
==，∴
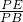=①，同理可得
=②，解关于①②的方程组，得
，故S△ABC=40+30+35+70+84+56=315．
分析：先设S△APE=x，S△BPF=y，根据同高不同底的两个三角形的面积比等于它们的底之比，可得
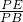==，从而有=①，同理可得=②，解①②组成的方程组，而S△ABC=S△BDP+S△CDP+S△CPE+S△APE+S△APF+S△BPF，易求其面积．点评：本题考查了三角形面积、解二元一次方程组．注意：同高不同底的两个三角形的面积比等于它们的底之比．
练习册系列答案
相关题目
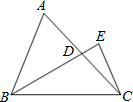如图所示，已知D为边AC的中点，CE垂直于BD的延长线于点E，CE=2cm，S△ABC=8cm2，则线段BD的长为
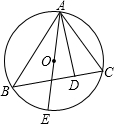如图所示，已知AE为⊙O的直径，AD为△ABC的BC边上的高．
如图所示，已知AB为⊙O的直径，点P为OA上一点，弦MN过点P，且AP=2，OP=3，MP=2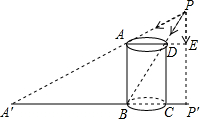
一圆柱形器皿在点光源P下的投影如图所示，已知AD为该器皿底面圆的直径，且AD=3，CD为该器皿的高，CD=4，CP′=1，点D在点P下的投影刚好位于器皿底与器皿壁的交界处，即点B处，点A在点P下的投影为A′，求点A′到CD的距离．
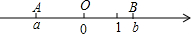在数轴上表示a，0，1，b四个数的点如图所示，已知O为AB的中点，求a+b+