题目内容
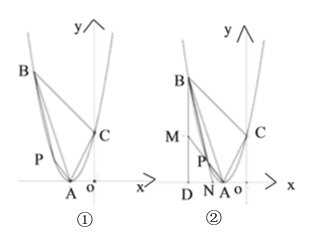
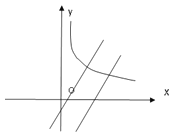
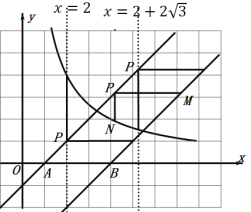
【题目】平面直角坐标系中,函数![]() (x>0),y=x-1,y=x-4的图象如图所示,p(a , b)是直线
(x>0),y=x-1,y=x-4的图象如图所示,p(a , b)是直线![]() 上一动点,且在第一象限.过P作PM∥x轴交直线
上一动点,且在第一象限.过P作PM∥x轴交直线![]() 于M,过P作PN∥y轴交曲线
于M,过P作PN∥y轴交曲线![]() 于N.
于N.
(1)当PM=PN时,求P点坐标
(2)当PM > PN时,直接写出a的取值范围.
【答案】(1)(2,1)或(![]() ,
,![]() );(2)
);(2)![]()
【解析】
(1)根据直线![]() 与直线
与直线![]() 的特征,可以判断
的特征,可以判断![]() 为平行四边形,且
为平行四边形,且![]() ,再根据坐标特征得到等式
,再根据坐标特征得到等式![]() =3 ,即可求解;
=3 ,即可求解;
(2)根据第(1)小题的结果结合图象即可得到答案.
(1)∵直线![]() 与
与![]() 轴交点
轴交点![]() ,直线
,直线![]() 与
与![]() 轴交点
轴交点![]() ,
,
∴![]() ,
,
∵直线![]() 与直线
与直线![]() 平行,
平行,
且![]() ∥
∥![]() 轴,
轴,
∴![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
∵![]() ∥
∥![]() 轴,
轴, ![]() 在
在![]() 的图象上,
的图象上,
∴![]() ,
,
∵![]() 在直线
在直线![]() 上 ,
上 ,
∴![]() ,
,
∵![]() ,
,
∴![]() =3 ,
=3 ,
解得:![]() 或
或![]() ,
,
(2)如图,
∵![]() 或
或![]() ,
,![]() ,
,
当点![]() 在直线
在直线![]() 和
和![]() 区间运动时,
区间运动时,![]() ,
,
∴![]()

练习册系列答案
相关题目