题目内容
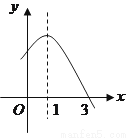
(14分)如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
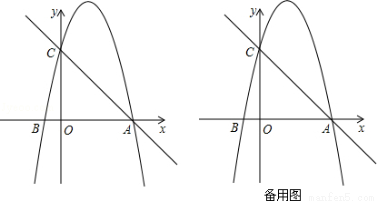
(1)求抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠PCO=∠POC?若存在,求出符合条件的点P的坐标;若不存在,说明理由;
(3)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(1)y=﹣x2+3x+4;(2)存在.点P的坐标是:( ,2)或(
,2)或( ,2);(3)存在.P的坐标是(2,6)或(﹣2,﹣6).
,2);(3)存在.P的坐标是(2,6)或(﹣2,﹣6).
【解析】
试题分析:(1)求出点BC的坐标,设抛物线的解析式是y=ax2+bx+c,将点A、B、C的坐标代入解方程再即可;(2)线段OC的垂直平分线l:y=2与抛物线y=﹣x2+3x+4的交点即为点P;(3)假设存在,分以C为直角顶点和点A为直角顶点,两种情况讨论即可.
试题解析:
【解析】
(1)由A(4,0),可知OA=4,
∵OA=OC=4OB,
∴OA=OC=4,OB=1,
∴C(0,4),B(﹣1,0).
设抛物线的解析式是y=ax2+bx+c,
则 ,
,
解得: ,
,
则抛物线的解析式是:y=﹣x2+3x+4; 4分
(2)存在. 5分
作线段OC的垂直平分线l,与抛物线的交点即为点P.
∵C(0,4),O(0,0),
∴直线l的表达式为y=2;.代入抛物线的表达式,
得2=﹣x2+3x+4; 6分
解得,x=
∴点P的坐标是:( ,2)或(
,2)或( ,2).............8分
,2).............8分
(3)存在. 9分
第一种情况,当以C为直角顶点时,过点C作CP1⊥AC,交抛物线于点P1.过点P1作y轴的垂线,垂足是M.
∵∠ACP1=90°,
∴∠MCP1+∠ACO=90°.
∵∠ACO+∠OAC=90°,
∴∠MCP1=∠OAC.
∵OA=OC,
∴∠MCP1=∠OAC=45°,
∴∠MCP1=∠MP1C,
∴MC=MP1,
设P(m,﹣m2+3m+4),则m=﹣m2+3m+4﹣4,
解得:m1=0(舍去),m2=2.
∴﹣m2+3m+4=6,
即P(2,6). 12分
第二种情况,当点A为直角顶点时,过A作AP2,AC交抛物线于点P2,过点P2作y轴的垂线,垂足是N,AP交y轴于点F.
∴P2N∥x轴,
由∠CAO=45°,
∴∠OAP=45°,
∴∠F P2N=45°,AO=OF.
∴P2N=NF,
设P2(n,﹣n2+3n+4),则n=(﹣n2+3n+4)+4
解得:n1=﹣2,n2=4(舍去),
∴﹣n2+3n+4=﹣6,
则P2的坐标是(﹣2,﹣6).
综上所述,P的坐标是(2,6)或(﹣2,﹣6); 14分

考点:1.待定系数法求解析式;2.两函数的交点坐标;3.一元二次方程;4.直角三角形的性质.

 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
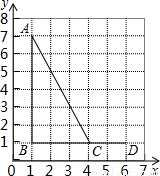


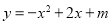 的部分图象如右图所示,则关于
的部分图象如右图所示,则关于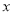 的一元二次方程
的一元二次方程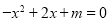 的解为__________。
的解为__________。