题目内容
在△ABC中,(2sinA-1)2+ =0,则△ABC的形状为________.
=0,则△ABC的形状为________.
直角三角形
分析:先根据非负数的性质及特殊教的三角函数值求出∠A、∠B的度数,再根据三角形的内角和定理求出∠C的度数,最后根据三个内角关系判断出其形状.
解答:∵(2sinA-1)2+ =0,
=0,
∴2sinA-1=0,cosB- =0,
=0,
∴sinA= ,∠A=30°;
,∠A=30°;
cosB= ,∠B=60°.
,∠B=60°.
∴∠C=90°.
∴△ABC是直角三角形.
点评:本题考查了:(1)特殊角的三角函数值;(2)非负数的性质;(3)三角形的内角和定理.
分析:先根据非负数的性质及特殊教的三角函数值求出∠A、∠B的度数,再根据三角形的内角和定理求出∠C的度数,最后根据三个内角关系判断出其形状.
解答:∵(2sinA-1)2+
 =0,
=0,∴2sinA-1=0,cosB-
 =0,
=0,∴sinA=
 ,∠A=30°;
,∠A=30°;cosB=
 ,∠B=60°.
,∠B=60°.∴∠C=90°.
∴△ABC是直角三角形.
点评:本题考查了:(1)特殊角的三角函数值;(2)非负数的性质;(3)三角形的内角和定理.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
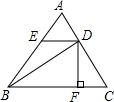 如图,在△ABC中,AC=15,BC=18,cosC=
如图,在△ABC中,AC=15,BC=18,cosC=| 3 |
| 5 |
| A、7.5 | B、9 | C、10 | D、5 |
 点停止,点Q从C点开始沿CB方向向点B以2m/s的速度移动,在点B停止.
点停止,点Q从C点开始沿CB方向向点B以2m/s的速度移动,在点B停止.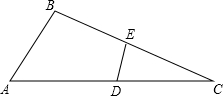 已知:如图,在△ABC中,E是BC的中点,D在AC边上,若AC长是1,且∠BAC=60°,∠ABC=100°,∠DEC=80°,求S△ABC+2S△CDE.
已知:如图,在△ABC中,E是BC的中点,D在AC边上,若AC长是1,且∠BAC=60°,∠ABC=100°,∠DEC=80°,求S△ABC+2S△CDE. 如图,在△ABC中,D是BC上任意一点,O是AD上任意一点,S△ABO=3,S△BOD=2S△ACO=1,那么S△COD=
如图,在△ABC中,D是BC上任意一点,O是AD上任意一点,S△ABO=3,S△BOD=2S△ACO=1,那么S△COD=