Question

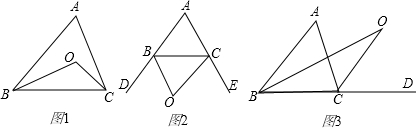
（1）如图1，BO、CO分别是△ABC中∠ABC和∠ACB的平分线，则∠BOC与∠A的关系是

90°+

1

2

∠A

（直接写出结论）；
（2）如图2，BO、CO分别是△ABC两个外角∠CBD和∠BCE的平分线，则∠BOC与∠A的关系是

90°-

1

2

∠A

，请证明你的结论．
（3）如图3，BO、CO分别是△ABC一个内角和一个外角的平分线，则∠BOC与∠A的关系是

1

2

∠A

，请证明你的结论．
（4）利用以上结论完成以下问题：如图4，已知：∠DOF=90°，点A、B分别是射线OF、OD上的动点，△ABO的外角∠OBE的平分线与内角∠OAB的平分线相交于点P，猜想∠P的大小是否变化？请证明你的猜想．

Answer 1

分析：（1）先根据三角形内角和定理求出∠ABC+∠ACB的度数，再根据BO、CO分别平分∠ABC与∠ACB求出∠1+∠2的度数，由三角形内角和定理即可得出∠BOC的度数；
（2）由三角形的一个外角等于与它不相邻的两个内角的和可证2∠1+2∠2=2∠A+∠ABC+∠ACB=∠A+180°，再根据三角形内角和定理可证2∠BOC=180°-∠A，即
∠BOC=90°-

1

2

∠A；
（3）根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB，然后再根据三角形的内角和定理列式整理即可得解；
（4）利用（3）中的解题思路证得∠P的大小不会变化始终为45°．

解答：解：（1）∠BOC=90°+

1

2

∠A．理由如下：
如图1，∵∠ABC+∠ACB=180°-∠A，BO、CO分别是∠ABC、∠ACB的角平分线，
∴∠1+∠2=

1

2

（∠ABC+∠ACB）=90°-

1

2

∠A，
∴∠BOC=180°-（∠1+∠2）=90°+

1

2

∠A；
故答案是：90°+

1

2

∠A；

（2）∠BOC=90°-

1

2

∠A．
证明：如图2，∵BD平分∠DBC，
∴∠OBC=

1

2

∠DBC．
同理可证：∠OCB=

1

2

∠BCE．
∴∠OBC+∠OCB=

1

2

（∠DBC+∠BCE），
∵∠DBC=∠A+∠ACB，∠BCE=∠A+∠ABC，
∴∠OBC+∠OCB=

1

2

（∠A+∠ACB+∠ABC+∠A）=

1

2

（180°+∠A）=90°+

1

2

∠A，
∴∠BOC=180°-（∠OBC+∠OCB）=90°-

1

2

∠A；
故答案是：90°-

1

2

∠A；

（3）∠BOC=

1

2

∠A；
证明：∵CO平分∠ACD    BO平分∠ABC
∴∠OCD=

1

2

∠ACD∠OBC=

1

2

∠ABC
∵∠OCD是△OBC的外角
∴∠BOC=∠OCD-∠OBC
=

1

2

（∠ACD-∠ABC）
∵∠ACD是△ABC的外角
∴∠ACD-∠ABC=∠A
∴∠BOC=

1

2

∠A；
故答案是：

1

2

∠A；

（4）∠P的大小没有变化．
根据（3）可得：∠P=

1

2

∠AOB
∵∠AOB=90°
∴∠P=45°
∴∠P的大小不会变化始终为45°．

点评：本题考查三角形外角的性质、角平分线线的性质及三角形的内角和定理，解答的关键是沟通外角和内角的关系．