Question

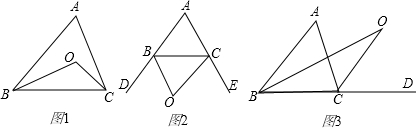
（1）如图1，BO、CO分别是△ABC中∠ABC和∠ACB的平分线，则∠BOC与∠A的关系是

 

；
（2）如图2，BO、CO分别是△ABC两个外角∠CBD和∠BCE的平分线，则∠BOC与∠A的关系是

 

；
（3）如图3，BO、CO分别是△ABC一个内角和一个外角的平分线，则∠BOC与∠A的关系是

 

．
（4）请就图2及图2中的结论进行证明．

Answer 1

分析：根据题意利用角平分线的性质及三角形内角和定理表示出两者的关系即可．

解答：解：（1）∠BOC=∠A+

1

2

（∠ABC+∠ACB）；

（2）∠BOC=180°-∠A-

1

2

（∠ABC+∠ACB）；

（3）∠BOC=

1

2

∠A；

（4）∵BO、CO分别是△ABC两个外角∠CBD和∠BCE的平分线，
∴∠CBO=

1

2

（∠A+∠ACB），∠BCO=

1

2

（∠A+∠ABC），
∴∠BOC=180°-∠CBO-∠BCO=180°-∠A-

1

2

（∠ABC+∠ACB），
∴∠BOC与∠A的关系是：∠BOC=180°-∠A-

1

2

（∠ABC+∠ACB）．

点评：此题主要考查学生对角平分线的性质及三角形内角和定理的综合运用能力．