题目内容
 如图所示,已知:AB=BC=AC,CD=DE=EC,
如图所示,已知:AB=BC=AC,CD=DE=EC,(1)求证:∠ACD=∠BCE;
(2)求证:△ADC≌BEC;
(3)求证:AD=BE.
分析:(1)根据△ABC和△CDE是等边三角形,依据等边三角形的每个角都是60°,即可证得∠ACB=∠DCE=60°,然后根据等式的性质即可证得;
(2)利用SAS即可证得;
(3)依据全等三角形的对应边相等即可证得.
(2)利用SAS即可证得;
(3)依据全等三角形的对应边相等即可证得.
解答:证明:(1)∵AB=BC=AC,CD=DE=EC,即△ABC和△CDE是等边三角形,
∴∠ACB=∠DCE=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
∴∠ACD=∠BCE;
(2)在△ADC和△BEC中,
,
∴△ADC≌△BEC;
(3)∵△ADC≌△BEC,
∴AD=BE.
∴∠ACB=∠DCE=60°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
∴∠ACD=∠BCE;
(2)在△ADC和△BEC中,
|
∴△ADC≌△BEC;
(3)∵△ADC≌△BEC,
∴AD=BE.
点评:本题考查了全等三角形的判定与性质,正确依据等边三角形的性质证得∠ACD=∠BCE是关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 24、如图所示,已知直线AB,CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ∥NP.为什么?
24、如图所示,已知直线AB,CD被直线EF所截,如果∠BMN=∠DNF,∠1=∠2,那么MQ∥NP.为什么? 3、如图所示,已知直线AB、CD交于点O,OE⊥AB于点O,且∠1比∠2大20°,则∠AOC=
3、如图所示,已知直线AB、CD交于点O,OE⊥AB于点O,且∠1比∠2大20°,则∠AOC=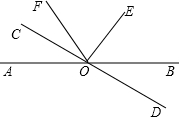 如图所示,已知直线AB和CD相交于点O,∠COE是直角,0F平分∠AOE.∠COF=34°.
如图所示,已知直线AB和CD相交于点O,∠COE是直角,0F平分∠AOE.∠COF=34°. 数轴上的点A,B,C的位置如图所示,已知线段AB的中点D与线段BC的中点E之间的距离为5,求点C对应的数.
数轴上的点A,B,C的位置如图所示,已知线段AB的中点D与线段BC的中点E之间的距离为5,求点C对应的数.