题目内容
1.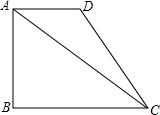 如图,在梯形ABCD中,AD∥BC,AB⊥BC,已知AD=2,cot∠ACB=$\frac{4}{3}$,梯形ABCD的面积是9;
如图,在梯形ABCD中,AD∥BC,AB⊥BC,已知AD=2,cot∠ACB=$\frac{4}{3}$,梯形ABCD的面积是9;(1)求AB的长;
(2)求tan∠ACD的值.
分析 (1)根据锐角三角函数设出边长,利用梯形的面积公式列方程即可;
(2)作DH⊥AC于H,利用三角形相似,列比例式求出DH=$\frac{6}{5}$,AH=$\frac{8}{5}$,CH=AC-AH=$\frac{17}{5}$,即可求出tan∠ACD=$\frac{DH}{CH}$=$\frac{6}{17}$.
解答 解:(1)在RtABC中,cot∠ACB=$\frac{BC}{AB}$=$\frac{4}{3}$,
设BC=4k,AB=3k,
∴S梯形ABCD=$\frac{1}{2}$(AD+BC)•AB=$\frac{1}{2}$(2+4k)•3k=9,
∴k=1或k=-$\frac{3}{2}$(舍),
∴AB=3;
(2)作DH⊥AC于H,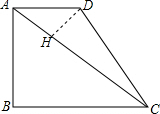
∵AD∥BC,
∴∠DAH=∠ACB,
∴△ADH∽△CAB,
∴$\frac{DH}{AB}$=$\frac{AD}{AC}$=$\frac{AH}{BC}$=$\frac{2}{5}$,
∴DH=$\frac{6}{5}$,AH=$\frac{8}{5}$,
∴CH=AC-AH=$\frac{17}{5}$,
∴tan∠ACD=$\frac{DH}{CH}$=$\frac{6}{17}$.
点评 本题考查了锐角三角函数,梯形的面积,相似三角形的判定和性质,作辅助线构造相似三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.在0,3,-1,$\frac{1}{2}$中最小的数是( )
| A. | 0 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |
 如图,直线l1∥l2,直线AB交直线l1,l2于D,B两点,AC⊥AB交直线l1于C.若∠1=40°40′,则∠2=130°40′.
如图,直线l1∥l2,直线AB交直线l1,l2于D,B两点,AC⊥AB交直线l1于C.若∠1=40°40′,则∠2=130°40′.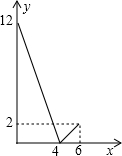 甲、乙两人分别从A、B两地同时出发,相向而行,相遇后,甲立即返回,乙的方向不变,且甲先到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系的图象如图所示,则甲的速度为:1.75千米/小时.
甲、乙两人分别从A、B两地同时出发,相向而行,相遇后,甲立即返回,乙的方向不变,且甲先到A地,两人相距的路程y(千米)与行驶时间x(小时)之间的函数关系的图象如图所示,则甲的速度为:1.75千米/小时.