题目内容
 如图,二次函数y1=ax2+bx+c(a≠0)的图象与一次函数y2=x+b的图象交于A(0,1),B两点.C(1,0)为二次函数图象的顶点.
如图,二次函数y1=ax2+bx+c(a≠0)的图象与一次函数y2=x+b的图象交于A(0,1),B两点.C(1,0)为二次函数图象的顶点.(1)求二次函数y1=ax2+bx+c(a≠0)的解析式;
(2)定义函数f:“当自变量x任取一值时,x对应的函数值分别为y1或y2,若y1≠y2,函数f的函数值等于y1、y2中的较小值;若y1=y2,函数f的函数值等于y1(或y2).”当直线y3=kx-
| 1 |
| 2 |
考点:待定系数法求二次函数解析式,一次函数的性质,二次函数的性质
专题:计算题
分析:(1)设抛物线解析式为y=a(x-1)2,将A坐标代入求出a的值,即可确定出解析式;
(2)联立抛物线与一次函数解析式求出B坐标,分①直线y=kx-
与直线AB:y=x+1平行;②直线y=kx-
过点B(3,4);③直线y=kx-
与二次函数y=x2-2x+1的图象只有一个交点,三种情况求出k的值即可.
(2)联立抛物线与一次函数解析式求出B坐标,分①直线y=kx-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)设抛物线解析式为y=a(x-1)2,
由抛物线过点A(0,1),可得y=x2-2x+1;
(2)将y=x2-2x+1与y=x+1联立解得:x=0,y=1或x=3,y=4,即B(3,4),
直线y=kx-
(k>0)与函数f的图象只有两个交点共有三种情况:
①直线y=kx-
与直线AB:y=x+1平行,此时k=1;
②直线y=kx-
过点B(3,4),此时k=
;
③直线y=kx-
与二次函数y=x2-2x+1的图象只有一个交点,
此时有
,
消元y得:x2-2x+1=kx-
,
由△=0,可得k1=
-2,k2=-
-2(舍去),
综上:k=1,k=
,k=
-2.
由抛物线过点A(0,1),可得y=x2-2x+1;
(2)将y=x2-2x+1与y=x+1联立解得:x=0,y=1或x=3,y=4,即B(3,4),
直线y=kx-
| 1 |
| 2 |
①直线y=kx-
| 1 |
| 2 |
②直线y=kx-
| 1 |
| 2 |
| 3 |
| 2 |
③直线y=kx-
| 1 |
| 2 |
此时有
|
消元y得:x2-2x+1=kx-
| 1 |
| 2 |
由△=0,可得k1=
| 6 |
| 6 |
综上:k=1,k=
| 3 |
| 2 |
| 6 |
点评:此题考查了待定系数法求二次函数解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
如果a、b互为相反数,c、d互为倒数,|m-1|=2.那么代数式:2003(a+b)2-4cd+
(a+b)2+6cd+m的值为( )
| 1 |
| 2 |
A、2006
| ||||
| B、4 | ||||
| C、5或1 | ||||
D、2006
|
有下列方程:①
=2;②
=
;③
=
+1;④
=1.其中是分式方程的有( )
| x+1 |
| 3 |
| 2 |
| x-1 |
| 1 |
| x+3 |
| x+2 |
| 3 |
| x-1 |
| 4 |
| 2 |
| x+3 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D、E,则△PDO≌△PEO的依据是( )
如图,∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为D、E,则△PDO≌△PEO的依据是( )| A、SSS | B、SAS |
| C、AAS | D、HL |
 如图,∠AOB=180°,OD是∠COB的平分线,OE是∠AOC的平分线,设∠BOD=α,则与α的余角相等的角是
如图,∠AOB=180°,OD是∠COB的平分线,OE是∠AOC的平分线,设∠BOD=α,则与α的余角相等的角是 如图,已知△ABC是等边三角形,D、E分别是AB、BC上的点,且AD=BE,连结CD、AE,CD与AE相交于点F.
如图,已知△ABC是等边三角形,D、E分别是AB、BC上的点,且AD=BE,连结CD、AE,CD与AE相交于点F.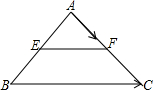 已知:如图,EF是△ABC的中位线,设
已知:如图,EF是△ABC的中位线,设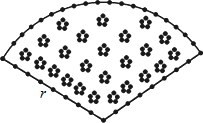 如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3)
如图,用长为20米的篱笆恰好围成一个扇形花坛,且扇形花坛的圆心角小于180°,设扇形花坛的半径为r米,面积为S平方米.(注:π的近似值取3) 如图,AB为⊙O的直径,射线AP交⊙O于C点,∠PCO的平分线交⊙O于D点,过点D作DE⊥AP交AP于E点.
如图,AB为⊙O的直径,射线AP交⊙O于C点,∠PCO的平分线交⊙O于D点,过点D作DE⊥AP交AP于E点.