题目内容
12.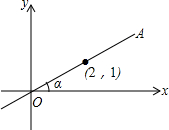 如图,在平面直角坐标系中,直线OA过点(2,1),则sinα的值是( )
如图,在平面直角坐标系中,直线OA过点(2,1),则sinα的值是( )| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 根据勾股定理求出OB的长,根据正弦的定义计算即可.
解答 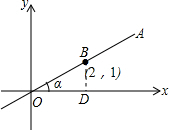 解:作BD⊥x轴于D,
解:作BD⊥x轴于D,
由题意得,OD=2,BD=1,
由勾股定理得,OB=$\sqrt{O{D}^{2}+B{D}^{2}}$=$\sqrt{5}$,
则sinα=$\frac{BD}{OB}$=$\frac{1}{\sqrt{5}}=\frac{\sqrt{5}}{5}$,
故选:B.
点评 本题考查的是锐角三角函数的定义,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
13.函数y=2x-1中,自变量x的取值范围是x>-1,则函数y的取值范围为( )
| A. | y<-3 | B. | y>-3 | C. | y>-1 | D. | y<-1 |
20.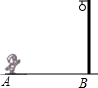 如图,小强晚上在路灯下散步,在由A处走到B处这一过程中,他在地上的影子( )
如图,小强晚上在路灯下散步,在由A处走到B处这一过程中,他在地上的影子( )
 如图,小强晚上在路灯下散步,在由A处走到B处这一过程中,他在地上的影子( )
如图,小强晚上在路灯下散步,在由A处走到B处这一过程中,他在地上的影子( )| A. | 逐渐变短 | B. | 逐渐变长 | C. | 先变短后变长 | D. | 先变长后变短 |
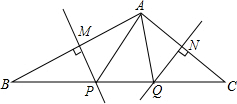 如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是40°.
如图,∠BAC=110°,若MP和NQ分别垂直平分AB和AC,则∠PAQ的度数是40°.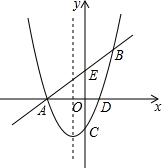 如图,已知抛物线与直线y=x+2交于A(-2,0)和B两点,与y轴交于C(0,-2),它的对称轴是直线x=-$\frac{1}{2}$,直线y=x+2与y轴交于点E.
如图,已知抛物线与直线y=x+2交于A(-2,0)和B两点,与y轴交于C(0,-2),它的对称轴是直线x=-$\frac{1}{2}$,直线y=x+2与y轴交于点E.