题目内容
2.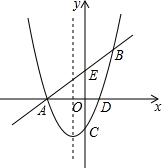 如图,已知抛物线与直线y=x+2交于A(-2,0)和B两点,与y轴交于C(0,-2),它的对称轴是直线x=-$\frac{1}{2}$,直线y=x+2与y轴交于点E.
如图,已知抛物线与直线y=x+2交于A(-2,0)和B两点,与y轴交于C(0,-2),它的对称轴是直线x=-$\frac{1}{2}$,直线y=x+2与y轴交于点E.(1)求抛物线与x轴的另一交点D的坐标及该抛物线对应的函数关系式;
(2)①求点B的坐标;②求证:E是AB的中点;
(3)若P(x,y)是该抛物线上的一个动点,是否存在这样的点P,使得PA=PB?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.
分析 (1)先根据对称性求出点D坐标,再利用待定系数法求出抛物线解析式.
(2)①列方程组即可解决;
②求出AE,EB即可判断.
(3)线段AB的垂直垂直平分线与抛物线的交点就是所求的点,求出线段AB的垂直平分线的解析式,然后解方程组即可.
解答 解:(1)∵点A(-2,0)是抛物线与x轴的交点,对称轴x=-$\frac{1}{2}$,
∴抛物线与x轴的另一个交点D为(1,0),
设抛物线为y=a(x+2)(x-1),把点C(0,-2)代入得a=1,
∴抛物线解析式为y=(x+2)(x-1)=x2+x-2.
(2)①由$\left\{\begin{array}{l}{y={x}^{2}+x-2}\\{y=x+2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$,
则点B坐标(2,4).
②∵点E坐标(0,2),点B(2.4),点A(-2,0),
∴AE=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,EB=$\sqrt{(0-2)^{2}+(2-4)^{2}}$=2$\sqrt{2}$,
∴AE=EB,
∴点E是AB中点.
(3)因为EA=EB,
所以过点E作线段AB的垂线与抛物线的交点就是所求的点P.
设过点E垂直AB的直线为y=-x+b,把点E(0,2)代入得到b=2,
∴过点E垂直AB的直线为y=-x+2,
由$\left\{\begin{array}{l}{y=-x+2}\\{y={x}^{2}+x-2}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-1+\sqrt{5}}\\{y=3-\sqrt{5}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1-\sqrt{5}}\\{y=3+\sqrt{5}}\end{array}\right.$,
∴点P坐标(-1+$\sqrt{5}$,3-$\sqrt{5}$)或(-1-$\sqrt{5}$,3+$\sqrt{5}$).
点评 本题考查二次函数、一次函数的有关知识、线段垂直平分线的性质等知识,学会用待定系数法确定函数解析式,知道求两个函数图象的交点转化为解方程组,两条直线垂直k1•k2=-1,本题体现了数形结合的思想,属于中考常考题型.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案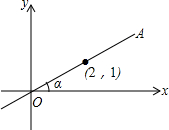 如图,在平面直角坐标系中,直线OA过点(2,1),则sinα的值是( )
如图,在平面直角坐标系中,直线OA过点(2,1),则sinα的值是( )| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
| A. |  | B. |  | C. |  | D. |  |
| A. | (a5)2=a10 | B. | 2a2•(-3a3)=-6a5 | C. | b•b5=b6 | D. | b5•b5=b25 |
 如图:
如图: