题目内容
 如图,以O为圆心,半径为2的圆与反比例函数y=
如图,以O为圆心,半径为2的圆与反比例函数y= (x>0)的图象交于A、B两点,则
(x>0)的图象交于A、B两点,则 的长度为
的长度为
- A.
 π
π - B.π
- C.
 π
π - D.
 π
π
D
分析:作AC⊥x轴,设A的坐标是:(a,b),在直角△OAC中,利用勾股定理以及A满足反比例函数的解析式,即可得到关于a,b的方程组求得A的坐标,从而求得∠AOC的度数,进而得到∠AOB的度数,利用弧长的计算公式即可求解.
解答: 解:作AC⊥x轴,设A的坐标是:(a,b),(其中a>0,b>0)
解:作AC⊥x轴,设A的坐标是:(a,b),(其中a>0,b>0)
根据题意得: ,
,
解得: ,
,
则AC=1,OC= ,
,
则∠AOC=30°,同理,OB与y轴正半轴的夹角是30°,
因而∠AOB=90°-30°-30°=30°,
则 的长度是:
的长度是: =
= .
.
故选D.
点评:本题是反比例函数与三角函数、弧长的计算的综合题,正确求得圆周角的度数是关键.
分析:作AC⊥x轴,设A的坐标是:(a,b),在直角△OAC中,利用勾股定理以及A满足反比例函数的解析式,即可得到关于a,b的方程组求得A的坐标,从而求得∠AOC的度数,进而得到∠AOB的度数,利用弧长的计算公式即可求解.
解答:
 解:作AC⊥x轴,设A的坐标是:(a,b),(其中a>0,b>0)
解:作AC⊥x轴,设A的坐标是:(a,b),(其中a>0,b>0)根据题意得:
 ,
,解得:
 ,
,则AC=1,OC=
 ,
,则∠AOC=30°,同理,OB与y轴正半轴的夹角是30°,
因而∠AOB=90°-30°-30°=30°,
则
 的长度是:
的长度是: =
= .
.故选D.
点评:本题是反比例函数与三角函数、弧长的计算的综合题,正确求得圆周角的度数是关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目




 如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.
如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.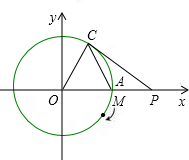 如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.
如图,以O为圆心,4为半径的圆与x轴交于点A,C在⊙O上,∠OAC=60°.
 时,求动点M所经过的弧长,并写出此时M点的坐标。
时,求动点M所经过的弧长,并写出此时M点的坐标。