题目内容
(1)如图1,正方形ABCD中,E,F,GH分别为四条边上的点,并且AE=BF=CG=DH.求证:四边形EFGH为正方形.(2)如图2,有一块边长1米的正方形钢板,被裁去长为
| 1 |
| 4 |
| 1 |
| 6 |
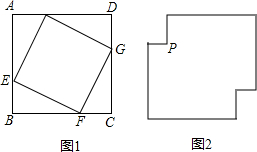 缘上,且P点在裁下的正方形一边上,问如何剪裁使得该正方形面积最大,最大面积是多少?
缘上,且P点在裁下的正方形一边上,问如何剪裁使得该正方形面积最大,最大面积是多少?
分析:(1)根据题意易得:△AEH≌△BFE≌△CGF≌△DHG,故四边形EFGH是菱形;又有∠4=90°,故四边形EFGH是正方形;
(2)先根据题意设原正方形为ABCD,正方形EFGH是要裁下的正方形,且AH=x;根据平行线的性质,得
=
;解得x的值,分别求出面积并比较大小可得答案.
(2)先根据题意设原正方形为ABCD,正方形EFGH是要裁下的正方形,且AH=x;根据平行线的性质,得
| ||
| x |
1-x-
| ||
| 1-x |
解答: (1)证明:∵AB=BC=CD=DA,AE=BF=CG=DH,
(1)证明:∵AB=BC=CD=DA,AE=BF=CG=DH,
∴EB=FC=GD=HA,
∵∠A=∠B=∠C=∠D=90°,
∴△AEH≌△BFE≌△CGF≌△DHG,(2分)
∴HE=EF=FG=GH,∠1=∠2,(3分)
∴四边形EFGH是菱形,(4分)
∵∠1+∠3=90°,
∴∠2+∠3=90°,
∴∠4=90°,
∴四边形EFGH是正方形;(5分)
(2)解:如图,设原正方形为ABCD,正方形EFGH是要裁下的正方形,且EH过点P.
设AH=x,则AE=1-x.
∵MP∥AH,
∴
=
,(6分)
整理得12x2-11x+2=0,
解得x1=
,x2=
,(7分)
当x=
时,S正方形EFGH=(
)2+(1-
)2=
,
当x=
时,S正方形EFGH=(
)2+(1-
)2=
<
,
∴当BE=DG=
米,BF=DH=
米时,裁下正方形面积最大,面积为
米2.(9分)
 (1)证明:∵AB=BC=CD=DA,AE=BF=CG=DH,
(1)证明:∵AB=BC=CD=DA,AE=BF=CG=DH,∴EB=FC=GD=HA,
∵∠A=∠B=∠C=∠D=90°,
∴△AEH≌△BFE≌△CGF≌△DHG,(2分)
∴HE=EF=FG=GH,∠1=∠2,(3分)
∴四边形EFGH是菱形,(4分)
∵∠1+∠3=90°,
∴∠2+∠3=90°,
∴∠4=90°,
∴四边形EFGH是正方形;(5分)
(2)解:如图,设原正方形为ABCD,正方形EFGH是要裁下的正方形,且EH过点P.

设AH=x,则AE=1-x.
∵MP∥AH,
∴
| ||
| x |
1-x-
| ||
| 1-x |
整理得12x2-11x+2=0,
解得x1=
| 1 |
| 4 |
| 2 |
| 3 |
当x=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 8 |
当x=
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 5 |
| 9 |
| 5 |
| 8 |
∴当BE=DG=
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 8 |
点评:解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,可有助于提高解题速度和准确率.

练习册系列答案
相关题目
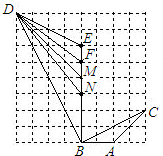 如图,在正方形网格上,与△ABC相似的三角形是( )
如图,在正方形网格上,与△ABC相似的三角形是( )| A、△NBD | B、△MBD | C、△EBD | D、△FBD |
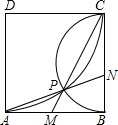 如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于( )
如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
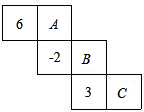 如图,是正方形的表面展形图,如果相对两个面数字之和相等,且A+B+C=14,则6A-2B+3C=
如图,是正方形的表面展形图,如果相对两个面数字之和相等,且A+B+C=14,则6A-2B+3C=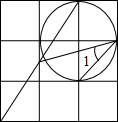 如图,在正方形网格图中,每个小正方形的边长均为 1,则∠1的正弦值是
如图,在正方形网格图中,每个小正方形的边长均为 1,则∠1的正弦值是 如图,在正方形ABCD中,E是BC上一点,且BC:EC=4:1,F是DC的中点.
如图,在正方形ABCD中,E是BC上一点,且BC:EC=4:1,F是DC的中点.