Question

9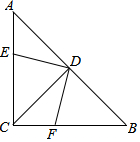．如图，在等腰直角△ABC中，∠ACB=90°，AC=BC，D为AB中点，DE⊥DF．
（1）写出图中所有全等三角形，分别为△AED≌△CFD；△CED≌△BFD；△ACD≌△BCD或△ACD≌△CBD．（用“≌”符号表示）
（2）求证：ED=DF．

Answer 1

分析 （1）利用等腰直角三角形的性质和三角形全等的判定解答即可；
（2）根据等腰直角三角形的性质和三角形全等的判定证明即可．

解答 解：（1）△AED≌△CFD；△CED≌△BFD；△ACD≌△BCD或△ACD≌△CBD；
故答案为：△AED≌△CFD；△CED≌△BFD；△ACD≌△BCD或△ACD≌△CBD；
（2）∵AC=BC，AD=BD，
∴∠CDA=90°，∠FCD=45°
∴AD=CD
∵∠CDA=∠ADE+∠EDC，
∠EDF=∠CDF+∠EDC．
∵∠EDF=∠CDA=90°，
∴∠ADE=∠CDF．
在△AED与△CFD中
$\left\{\begin{array}{l}{∠ADE=∠CDF}\\{AD=CD}\\{∠FCD=∠A=45°}\end{array}\right.$，
∴△AED≌△CFD
∴DE=DF．

点评 本题考查了等腰直角三角形的性质和全等三角形的判定与性质，关键是根据等腰直角三角形的性质和三角形全等的判定证明．