题目内容
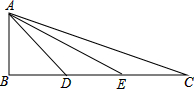如图，在△ABC，∠B=90°，AB=BD=DE=EC，则下列结论中成立的是（ ）| A、△ACD∽△EAD |
| B、△ABD∽△ABC |
| C、△ABE∽△ABC |
| D、△ABE∽△ACD |
考点：相似三角形的判定
专题：
分析：利用已知得出三角形对应边关系进而利用相似三角形的判定得出即可．
解答：解：∵在△ABC，∠B=90°，AB=BD=DE=EC，
∴AD=
BD，
∴
=
=
=
，
又∵∠ADE=∠CDA，
∴△ADE∽△CDA，
故选：A．
∴AD=
| 2 |
∴
| AD |
| CD |
| DE |
| AD |
| 1 | ||
|
| ||
| 2 |
又∵∠ADE=∠CDA，
∴△ADE∽△CDA，
故选：A．
点评：此题主要考查了相似三角形的判定，得出
=
是解题关键．
| AD |
| CD |
| DE |
| AD |
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
如图，已知AB∥CD，∠A=75°，则∠1的度数是（ ）| A、75° | B、105° |
| C、115° | D、15° |
下面说法正确的有（ ）
①π的相反数是-3.14；
②符号相反的数互为相反数；
③-（-3.8）的相反数是3.8；
④一个数和它的相反数不可能相等；
⑤正数与负数互为相反数；
⑥绝对值等于其本身的有理数只有零；
⑦相反数等于其本身的有理数只有零；
⑧倒数等于其本身的有理数只有1．
①π的相反数是-3.14；
②符号相反的数互为相反数；
③-（-3.8）的相反数是3.8；
④一个数和它的相反数不可能相等；
⑤正数与负数互为相反数；
⑥绝对值等于其本身的有理数只有零；
⑦相反数等于其本身的有理数只有零；
⑧倒数等于其本身的有理数只有1．
| A、0个 | B、1个 | C、2个 | D、3个 |
已知两圆半径分别是方程x2-4x+3=0的两根，两圆圆心距为2，则两圆位置关系是（ ）
| A、外切 | B、相交 | C、内切 | D、外离 |
