Question

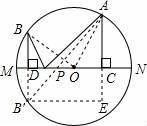
如图，MN为⊙O的直径，A、B是⊙O上的两点，过A作AC⊥MN于点C，过B作BD⊥MN于点D，P为DC上的任意一点，若MN=20，AC=8，BD=6，则PA+PB的最小值是　　　　　　．                   

                                                                          

Answer 1

14　．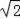                                                                                          

                                                                                                        

【考点】轴对称-最短路线问题；勾股定理；垂径定理．                                 

【专题】压轴题；探究型．                                                                     

【分析】先由MN=20求出⊙O的半径，再连接OA、OB，由勾股定理得出OD、OC的长，作点B关于MN的对称点B′，连接AB′，则AB′即为PA+PB的最小值，B′D=BD=6，过点B′作AC的垂线，交AC的延长线于点E，在Rt△AB′E中利用勾股定理即可求出AB′的值．                                                                        

【解答】解：∵MN=20，                                                                        

∴⊙O的半径=10，                                                                            

连接OA、OB，                                                                                  

在Rt△OBD中，OB=10，BD=6，                                                            

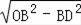
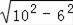
∴OD===8；                                                     

同理，在Rt△AOC中，OA=10，AC=8，                                                 

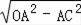
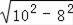
∴OC===6，                                                     

∴CD=8+6=14，                                                                                 

作点B关于MN的对称点B′，连接AB′，则AB′即为PA+PB的最小值，B′D=BD=6，过点B′作AC的垂线，交AC的延长线于点E，                                                                                                

在Rt△AB′E中，                                                                                

∵AE=AC+CE=8+6=14，B′E=CD=14，                                                      

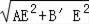
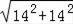
∴AB′===14．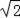                                            

故答案为：14．                                                                            

                                                                          

【点评】本题考查的是轴对称﹣最短路线问题、垂径定理及勾股定理，根据题意作出辅助线，构造出直角三角形，利用勾股定理求解是解答此题的关键．