Question

9．如图，Rt△OAB中，BA⊥OA，且OA=BA=4，点P从O点出发，沿OA以每秒1个单位的速度向A点移动，到达A点停止运动，则△OBP面积S与点P的运动时间t之间的函数图象大致是（　　）

• A．
• B．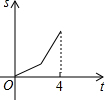
• C．
• D．

Answer 1

分析 根据点P的运动速度可得出OP=t，再根据三角形的面积公式得出S_△OPB=S=$\frac{1}{2}$OP•AB，确定S是t的正比例函数，画出图象即可．

解答 解：∵OP=t，OA=BA=4，
∴S_△OPB=S=$\frac{1}{2}$OP•AB=2t，
∵P点到达A点停止运动，
∴0＜OP＜4，
∴S是t的正比例函数，且0＜t＜4．
故选A．

点评 本题考查了动点问题的函数图象，以及直角三角形的面积公式，属于综合性的题目，对于此类动点型题目，首先要确定符合题意的条件下动点所在的位置，然后用时间t表示出有关线段的长度，进而建立关于线段的关系式，难度较大．