题目内容
如图，在一条长90米，宽为60米的矩形草地上修三条小路，小路都等宽，除小路外，草地面积为5192米2的6个矩形小块，则小路的宽度应为多少？考点：一元二次方程的应用
专题：几何图形问题
分析：设小路的宽为x米，草地的长为（90-2x）米，草地的宽为（60-x）米，根据草地的总面积为5192米2建立方程求出其解即可．
解答：解：设小路的宽为x米，草地的长为（90-2x）米，草地的宽为（60-x米），由题意，得
（90-2x）（60-x）=5192，
解得：x1=1，x2=104（舍去）．
答：小路的宽度应为1米．
（90-2x）（60-x）=5192，
解得：x1=1，x2=104（舍去）．
答：小路的宽度应为1米．
点评：本题考查了矩形的面积公式的运用，列一元二次方程解实际问题的运用，一元二次方程的解法的运用，解答时由矩形的面积=长×宽建立方程是关键．
练习册系列答案
相关题目
如图，圆的周长为4个单位长度，在圆的4等分点处标上0，1，2，3．先让圆周上数字0所对应的数与数轴上的数-1所对应的点重合，再让数轴按逆时针方向绕在该圆上，那么数轴上的数-2007将与圆周上的数字把一次函数y=3x-1的图象向上平移3个单位，可得到的图象的函数解析式是（ ）
| A、y=3x+3 |
| B、y=3x+2 |
| C、y=3x-4 |
| D、y=3x-2 |
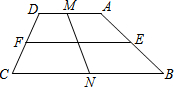如图，梯形ABCD中，AD∥BC，∠B=30°，∠C=60°，E、F、M、N分别为AB、CD、BC、DA的中点，若BC=7，MN=3，则EF为（ ）
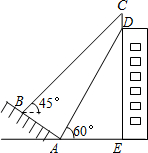如图，某校一幢教学大楼的顶部竖有一块宣传牌CD=2米．小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°，沿山坡向上走到B处测得宣传牌顶部C的仰角为45°．已知山坡AB的坡度i=1：
由物理学知识可知：在力F（牛）的作用下，物体会在力F的方向发生位移S（米），力F所做的功W（焦），满足W=FS，当W为定值时，F与S之间的函数图象如图．