题目内容
20. 如图,四边形ABCD内接于圆O,四边形ABCO是平行四边形,则∠ADC=60°.
如图,四边形ABCD内接于圆O,四边形ABCO是平行四边形,则∠ADC=60°.
分析 设∠ADC的度数=α,∠ABC的度数=β,由题意可得$\left\{\begin{array}{l}{α+β=180°}\\{α=\frac{1}{2}β}\end{array}\right.$,求出β即可解决问题.
解答 解:设∠ADC的度数=α,∠ABC的度数=β;
∵四边形ABCO是平行四边形,
∴∠ABC=∠AOC;
∵∠ADC=$\frac{1}{2}$β,∠AOC=α;而α+β=180°,
∴$\left\{\begin{array}{l}{α+β=180°}\\{α=\frac{1}{2}β}\end{array}\right.$,
解得:β=120°,α=60°,∠ADC=60°,
故答案为:60°.
点评 该题主要考查了圆周角定理及其应用问题;应牢固掌握该定理并能灵活运用.

练习册系列答案
相关题目
10.下列各式中,与3-19+5的值相等的是( )
| A. | 3+(-19)-(-5) | B. | -3+(-19)+(-5) | C. | -3+(-19)+5 | D. | 3-(+19)-(+5) |
15. 平行四边形ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
平行四边形ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
 平行四边形ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )
平行四边形ABCD中,AC,BD是两条对角线,如果添加一个条件,即可推出平行四边形ABCD是矩形,那么这个条件是( )| A. | AB=BC | B. | AC=BD | C. | AC⊥BD | D. | AB⊥BD |
5.下列各数中,负数是( )
| A. | (-5)2 | B. | -(-5) | C. | -|-5| | D. | -(-5)3 |
12.下列因式分解结果正确的是( )
| A. | 10a3+5a2=5a(2a2+a) | B. | 4x2-9=(4x+3)(4x-3) | ||
| C. | a2-4ab+4b2=(a-2b)2 | D. | x2-5x-6=x(x-5)-6 |
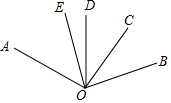 如图,OC,OD,OE是∠AOB内的射线,OD平分∠AOB,OC平分∠BOD,∠DOE=$\frac{1}{3}$∠AOE,若∠COE=45°,求∠AOB的度数.
如图,OC,OD,OE是∠AOB内的射线,OD平分∠AOB,OC平分∠BOD,∠DOE=$\frac{1}{3}$∠AOE,若∠COE=45°,求∠AOB的度数.