题目内容
19．
如图所示，BD与CD分别平分∠ABC和∠ACB，∠A=90°，求∠BDC的度数．
分析 首先根据三角形内角和是180°，求出∠ABC、∠ACB的度数和是多少；然后根据三角形的角平分线的性质，用∠ABC、∠ACB的度数和除以2，求出∠DBC、∠DCB的度数和是多少；最后用180°减去∠DBC、∠DCB的度数和，求出∠BDC的度数是多少即可．
解答 解：∵∠A=90°，
∴∠ABC+∠ACB
=180°-∠A
=180°-90°
=90°
∴∠DBC+∠DCB
=90°÷2
=45°
∴∠BDC
=180°-（∠DBC+∠DCB）
=180°-45°
=135°
即∠BDC的度数是135°．
点评 此题主要考查了三角形内角和定理的应用，以及三角形的角平分线的性质，要熟练掌握，解答此题的关键是求出∠DBC、∠DCB的度数和是多少．
练习册系列答案
相关题目
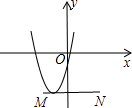如图，线段MN在平面直角坐标系中，点M，N的坐标分别为（-2，-4），（3，-4），抛物线y=ax2+bx+c（a＞0）顶点在线段MN上运动，该抛物线与x轴交于点C，D（点C在点D的左侧），下列结论中：①c≥-3；②当x＞4时，y随x的增大而增大；③若点C的横坐标的最小值为-4，则点D的横坐标最小值为0，其中正确的有（ ）
14．不等式组$\left\{\begin{array}{l}{2x-1＞0}\\{x+5≥4}\end{array}\right.$的解集是（ ）
| A． | x＞$\frac{1}{2}$ | B． | -1≤x＜$\frac{1}{2}$ | C． | x＜$\frac{1}{2}$ | D． | x≥-1 |
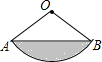如图，∠AOB=120°，OA=2，求S阴影．