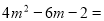题目内容
现定义运算“★”,对于任意实数 、
、 ,都有
,都有 ★
★ =
= ,如:3★5=
,如:3★5= ,若
,若 ★2=6,则实数
★2=6,则实数 的值是
的值是
4,-1
【解析】
试题分析:根据题中的新定义将所求式子转化为一元二次方程,求出一元二次方程的解即可得到x的值.
解:根据题中的新定义将x★2=6变形得:
x2-3x+2=6,即x2-3x-4=0,
因式分解得:(x-4)(x+1)=0,
解得:x1=4,x2=-1,
则实数x的值是-1或4.
故答案为:4,-1
考点:解一元二次方程-因式分解法.
考点分析: 考点1:一元二次方程 定义:只含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
一元二次方程的一般形式:

它的特征是:等式左边是一个关于未知数x的二次多项式,等式右边是零,其中 ax2叫做二次项,a叫做二次项系数;bx叫做一次项,b叫做一次项系数;c叫做常数项。 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 ,
, 是一元二次方程
是一元二次方程 的两个实数根.
的两个实数根. 的取值范围;
的取值范围; ,且
,且

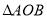 为等腰三角形,顶点
为等腰三角形,顶点 的坐标(2,
的坐标(2, ),底边OB在
),底边OB在 轴上.将
轴上.将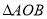 绕点
绕点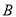 按顺时针方向旋转一定角度后得
按顺时针方向旋转一定角度后得 ,点
,点 的对应点
的对应点 在
在 轴上,则点
轴上,则点 的坐标为
的坐标为 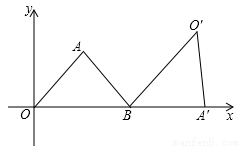
 是关于
是关于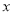 的方程
的方程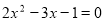 的一根,代数式
的一根,代数式