题目内容
如图，正方形ABCD的两条对角线把正方形分割成四个等腰直角三角形，将这四个三角形分别沿正方形ABCD的边向外翻折，可得到一个新正方形EFGH．请你在矩形ABCD中画出分割线，将矩形分割成四个三角形，然后分别将这四个三角形沿矩形的边向外翻折，使得图1得到菱形，图2得到矩形，图3得到一般的平行四边形（只在矩形ABCD中画出分割线，说明分割线的作法，不画出翻折后的图形）．
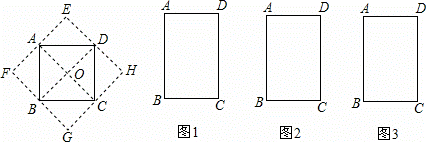
解：如图所示：
得到菱形的分割线做法：连结矩形ABCD的对角线AC、BD（把原矩形分割为四个全等的等腰三角形）；
得到矩形的分割线做法：连结矩形ABCD的对角线BD，分别过点A、C作AE⊥BD于E，CF⊥BD于F（把原矩形分割为四个直角三角形）；
得到平行四边形的分割线做法：连结矩形ABCD的对角线BD，分别过点A、C作AE∥CF，分别交BD于E、F（把原矩形分割为四个三角形）．
点评： 此题主要考查了应用设计与作图，正确利用各图形的性质得出是解题关键．
练习册系列答案
相关题目
CD中，∠B＝∠BCD＝90°，AB＝BC．
三角形ABC”（如图（2）），N是∠ACP的平分线上一点，则当∠AMN＝60°时，结论AM＝MN是否还成立？请说明理由．
B. 
C.
D
化成
的形式后为 ，其一次项系数与常数项的和为 。
向右平移一个单位长度，再向上平移3个单位长度后，所得抛物线的解析式为（ ）
B、
C、
D、
的对称轴为 ，顶点坐标为 ，它的最高（低）点在 点，当
时，它有最大（小）值，值为 。