题目内容
如图,四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点.
(1)判断四边形EFGH是何种特殊的四边形,并说明你的理由;
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是 AD=BC .
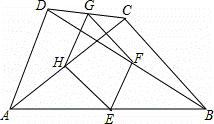
解:(1)四边形EFGH是平行四边形;
证明:在△ACD中∵G、H分别是CD、AC的中点,
∴GH∥AD,GH= AD,
在△ABC中∵E、F分别是AB、BD的中点,
∴EF∥AD,EF= AD,
∴EF∥GH,EF=GH,
∴四边形EFGH是平行四边形.
(2)要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是AD=BC.
理由如下:∵E,F分别是AB,BD的中点,
∴EF∥AD且EF= AD,
同理可得:GH∥AD且GH= AD,EH∥BC且EH= BC,
∴EF∥GH且EF=GH,
∴四边形EFGH是平行四边形,
∵AD=BC,
∴ AD= BC,
即EF=EH,
∴▱EFGH是菱形.

练习册系列答案
相关题目
 形ABCD为菱形的是( ).
形ABCD为菱形的是( ).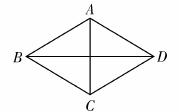

 中,自变量x的取值范围是( )
中,自变量x的取值范围是( ) ≠3 B.
≠3 B.
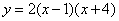 ; (2)
; (2) 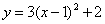 ;(3)
;(3)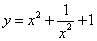 ; (4)
; (4)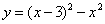 .不是二次函数的是( )
.不是二次函数的是( ) 的对称轴为 ,顶点坐标为 。
的对称轴为 ,顶点坐标为 。 ,且抛物线
,且抛物线 的形状、开口方向都相同的抛物线的解析式为 。
的形状、开口方向都相同的抛物线的解析式为 。