题目内容
若∠AOB=90°,∠BOC=40°,则∠AOB的平分线与∠BOC的平分线的夹角等于( )A.65°
B.25°
C.65°或25°
D.60°或20°
【答案】分析:本题分两种情况讨论:(1)当OC在三角形内部;(2)当OC在三角形外部.根据三角形的角平分线及角的和差关系求解.
解答: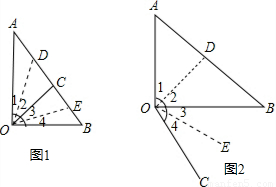 解:本题分两种情况讨论:
解:本题分两种情况讨论:
(1)当OC在三角形内部时,如图1,
∵∠AOB=90°,∠BOC=40°,OD,OE是∠AOB的与∠BOC的平分线,
∴∠AOD=∠DOB= ∠AOB=
∠AOB= ×90°=45°,∠BOE=∠EOC=
×90°=45°,∠BOE=∠EOC= ∠BOC=
∠BOC= ×40°=20°,
×40°=20°,
∴∠DOE=∠DOB-∠EOB=45°-20°=25°;
(2)当OC在三角形外部时,如图2,
∵∠AOB=90°,∠BOC=40°,OD,OE是∠AOB的与∠BOC的平分线,
∴∠AOD=∠DOB= ∠AOB=
∠AOB= ×90°=45°,∠BOE=∠EOC=
×90°=45°,∠BOE=∠EOC= ∠BOC=
∠BOC= ×40°=20°,
×40°=20°,
∴∠DOE=∠DOB+∠EOB=45°+20°=65°.
故选C.
点评:本题较简单,考查的是三角形的角平分线及角的和差关系,在解答此题时要注意分两种情况讨论,不要漏解.
解答:
 解:本题分两种情况讨论:
解:本题分两种情况讨论:(1)当OC在三角形内部时,如图1,
∵∠AOB=90°,∠BOC=40°,OD,OE是∠AOB的与∠BOC的平分线,
∴∠AOD=∠DOB=
 ∠AOB=
∠AOB= ×90°=45°,∠BOE=∠EOC=
×90°=45°,∠BOE=∠EOC= ∠BOC=
∠BOC= ×40°=20°,
×40°=20°,∴∠DOE=∠DOB-∠EOB=45°-20°=25°;
(2)当OC在三角形外部时,如图2,
∵∠AOB=90°,∠BOC=40°,OD,OE是∠AOB的与∠BOC的平分线,
∴∠AOD=∠DOB=
 ∠AOB=
∠AOB= ×90°=45°,∠BOE=∠EOC=
×90°=45°,∠BOE=∠EOC= ∠BOC=
∠BOC= ×40°=20°,
×40°=20°,∴∠DOE=∠DOB+∠EOB=45°+20°=65°.
故选C.
点评:本题较简单,考查的是三角形的角平分线及角的和差关系,在解答此题时要注意分两种情况讨论,不要漏解.

练习册系列答案
相关题目
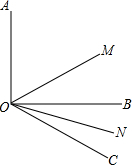 如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
 如图,已知圆O的半径OA=2,C为半径OB的中点,若∠AOB=90°,则图中阴影部分的面积为
如图,已知圆O的半径OA=2,C为半径OB的中点,若∠AOB=90°,则图中阴影部分的面积为