题目内容
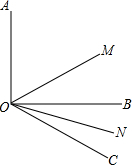 如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.
如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC.(1)若∠AOB=90°,∠BOC=30°,则∠MON=
(2)若∠AOB=80°,∠BOC=30°,则∠MON=
(3)根据本题,请你提出一个与∠MON的度数有关的结论,并加以说明.
分析:(1)和(2)中,根据角平分线的概念以及结合图形利用角的和差关系进行计算;
(3)中由上述计算的过程即可发现角之间的关系.
(3)中由上述计算的过程即可发现角之间的关系.
解答:解:(1)∵∠AOB=90°,∠BOC=30°,
∴∠AOC=120°.
又OM平分∠AOC,ON平分∠BOC,
∴∠COM=60°,∠CON=15°.
∴∠MON=45°.
(2)∵∠AOB=80°,∠BOC=30°,
∴∠AOC=110°.
又OM平分∠AOC,ON平分∠BOC,
∴∠COM=55°,∠CON=15°
∴∠MON=40°.
(3)∠MON的度数等于∠AOB度数的一半.
设∠AOB=α,∠BOC=β,
∠MOC=
(α+β),∠CON=
β,
所以∠MON=∠MOC-∠CON=
(α+β)-
β=
.
∴∠AOC=120°.
又OM平分∠AOC,ON平分∠BOC,
∴∠COM=60°,∠CON=15°.
∴∠MON=45°.
(2)∵∠AOB=80°,∠BOC=30°,
∴∠AOC=110°.
又OM平分∠AOC,ON平分∠BOC,
∴∠COM=55°,∠CON=15°
∴∠MON=40°.
(3)∠MON的度数等于∠AOB度数的一半.
设∠AOB=α,∠BOC=β,
∠MOC=
| 1 |
| 2 |
| 1 |
| 2 |
所以∠MON=∠MOC-∠CON=
| 1 |
| 2 |
| 1 |
| 2 |
| α |
| 2 |
点评:此题要能够根据图形表示角之间的和与差,能够根据角平分线的概念用几何式子表示角之间的倍分关系.注意由特殊推广到一般,发现并总结结论.

练习册系列答案
相关题目
 25、如图所示,已知AO⊥BC于O,DO⊥OE,∠1=65°,求∠2的度数.
25、如图所示,已知AO⊥BC于O,DO⊥OE,∠1=65°,求∠2的度数.
 如图所示,已知AO⊥BC于O,DO⊥OE,∠1=65°,求∠2的度数.
如图所示,已知AO⊥BC于O,DO⊥OE,∠1=65°,求∠2的度数.
